大阪大学大学院基礎工学研究科の小林舜典助教と垂水竜一教授は、らせん転位によって生み出される結晶格子の乱れが結晶格子の中で力へ変換されるメカニズムを数学的に解明しました。らせん転位は結晶材料の強度や延性を決定する重要なトポロジカル欠陥の一つですが、その力学的な性質に関する研究は十分進んでおらず、多くの研究課題が残されていました。

今回、垂水教授らの研究グループでは、らせん転位の理論解析に微分幾何学を用いることによって、(i)らせん転位の中心には「リッチ曲率」と呼ばれる結晶空間のゆがみが存在すること、(ii)リッチ曲率は通常の結晶空間（ユークリッド空間）と非整合な「幾何学的なフラストレーション」状態を生み出すこと、(iii)フラストレート状態の解消に必要な弾性変形が力の起源となること、を明らかにしました。

本研究の成果は、2024年12月4日（水）に英国王立協会誌「Royal Society Open Science」により公開されました。

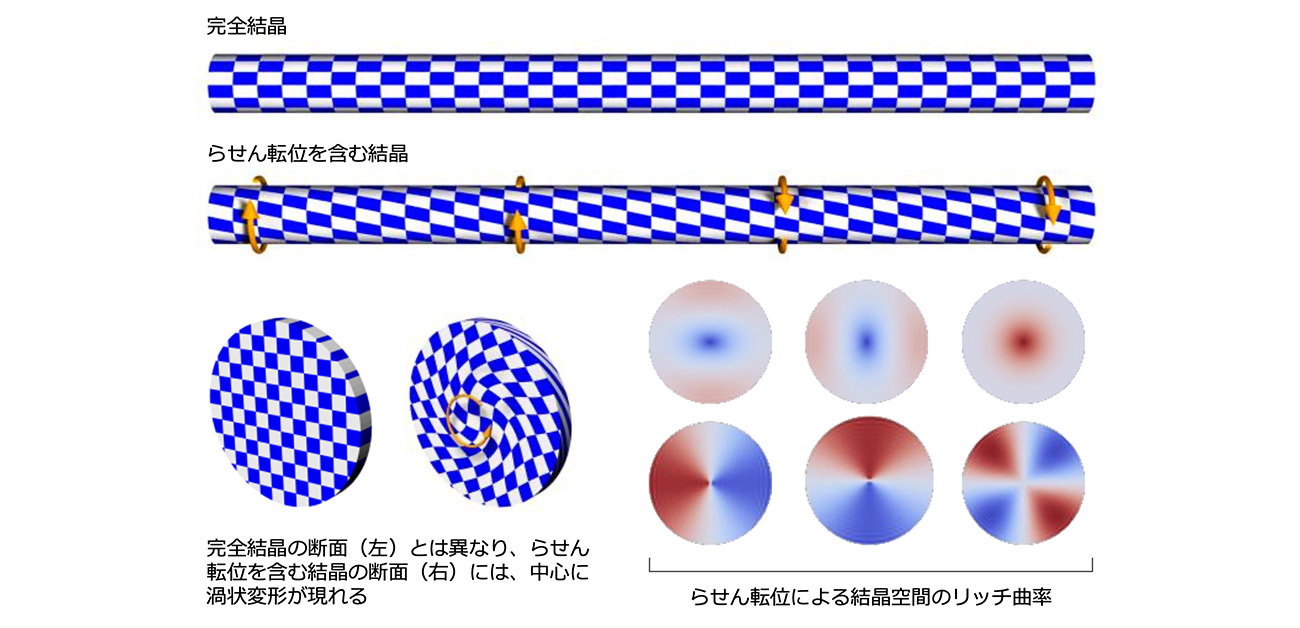
図. らせん転位によって生じる結晶格子の乱れの模式図（上段、下段左）と、それを定量的に表した空間のリッチ曲率の数値解析結果（下段右、六つの独立成分を表示しており、色の濃さが曲率の大きさに対応する）

トポロジカル欠陥の一種であるらせん転位はその中心付近に渦状構造を持つが、これが周辺の結晶と幾何学的に非整合となり、その解消のため結晶中には弾性的な復元力が発生する。

結晶材料の内部には「転位」と呼ばれる結晶格子の乱れた領域（トポロジカル格子欠陥）が存在します。転位による乱れの大きさは原子面1層程度のとても小さなものですが、外力を負荷された結晶の内部では転位がすべり運動を起こし、その過程で無数の増殖を繰り返すことから、大きな塑性変形（物体に外力を加えて変形させ、その後、外力を取り去っても元に戻らない変形）が可能となります。この転位運動と増殖機構に起因して、現実の結晶材料が発揮できる強度は理論的に予測される値の1,000分の1程度に留まります。そのため、結晶材料の効率的な設計には、転位とその周辺に形成される力学場の理解が極めて重要となります。転位に関する従来の研究では、主に電子顕微鏡法による転位構造の精密観察や、第一原理・分子動力学法による計算機シミュレーションが用いられてきました。これらの研究では、転位による結晶格子の乱れや、それに起因した力の空間的な広がり方を評価することはできますが、そもそもなぜ転位はその周辺の結晶格子に力を生み出すのか？という最も本質的な疑問に答えることはできませんでした。結晶格子の内部で転位が生み出す力は、局所的には数百MPa（メガパスカル）という高いオーダーに到達します。またこの力は、ひとたび転位が形成されると残存し、外力を取り除いても決して消えることはありません。結晶の内部に閉じこめられた力の起源は何か？この疑問はVolterraによって転位の概念が提案されてから1世紀以上経過した現代においても、未解決のまま残された大きな研究課題の一つでした。

小林助教と垂水教授の研究グループでは、これまで微分幾何学に基づく転位論の一般化に関する理論研究を進めてきました。微分幾何学は、空間の長さや角度を自由に調整することができるやわらかい幾何学の総称です。微分幾何学がもたらす解析空間の飛躍的な拡張は、転位による結晶格子の乱れを数学的に表現する上で最適な枠組みを提供します。しかしながら、微分幾何学と転位論の融合にはリーマン・カルタン多様体と呼ばれる抽象的な数学が必要となることから、解析の参入障壁が高く、これまで材料科学分野では全く応用されていませんでした。

今回、垂水教授らの研究グループでは、リーマン・カルタン多様体を用いたらせん転位の定式化に成功するとともに、得られた理論をアイソジオメトリック解析と呼ばれる数値計算法へ実装することによって、らせん転位の中心に形成される渦状変形に着目した数値解析を行いました。その結果、渦状変形領域には「リッチ曲率」と呼ばれる結晶空間のゆがみが存在するとともに、これが通常の結晶空間（ユークリッド空間）に対して非整合となる、いわゆる「幾何学的なフラストレーション」状態が生み出されていることを明らかにしました。また、フラストレーション状態の解消にはリッチ曲率と逆の曲率を持つ弾性変形が必要になりますが、これが結晶格子に力を生み出す直接的な起源となること、またらせん転位はトポロジカル欠陥として位相幾何学的に安定していることから、その周辺では弾性的な復元力が働き続けることを明らかにしました。「結晶空間の曲率が力を生み出す」という本研究の理論的な結論は、宇宙空間の曲率と重力を結びつけた相対性理論と数学的に類似しており、今後は両理論の数理構造に着目した研究展開が期待されます。

現代社会を支える構造材料の大半は、金属材料（鉄鋼材料やアルミニウム合金など）を中心とした結晶材料によって作られています。結晶材料の強度は転位の力学的な性質によって決まることから、結晶の内部で転位が力を生み出すメカニズムの解明は、結晶材料の強度の本質に迫る極めて重要な研究課題でした。この問題を数学的な立場から解明した本研究の成果は、全ての結晶材料に対して適用することができます。今後は、様々な構造材料の効率的な設計に応用可能と考えられます。

本研究の成果は、2024年12月4日（水）に英国王立協会誌「Royal Society Open Science」（オンライン）に掲載されました。

タイトル：“Geometrical frustration in nonlinear mechanics of screw dislocation”
著者名：Shunsuke Kobayashi and Ryuichi Tarumi
ＤＯＩ：https://doi.org/10.1098/rsos.240711

なお、本研究は、科学技術振興機構（JST）戦略的創造研究推進事業さきがけ（課題番号：JPMJPR1997）および日本学術振興会科学研究費助成事業（課題番号：JP18H05481, JP23K13221, 24K00761）の支援を受けて実施されました。

垂水研究室 Webページ
https://nonlinear-solidmechanics.org/