大阪大学大学院基礎工学研究科 小林舜典助教、垂水竜一教授らの研究グループは、結晶の中にある「転位」という欠陥が生み出す結晶格子の歪みのパターンが、電流が作り出す磁場のパターンと同型になることを発見しました。

転位は、結晶材料の強度と柔軟性を決める重要な欠陥の一つですが、その力学的な性質に関する理論研究は十分進んでおらず、多くの研究課題が残されていました。

今回、研究グループでは、①転位の周りに作られる塑性変形（物体に外力を加えて変形させ、その後、外力を取り去っても残る変形）による歪みのパターン（カルタン方程式）が、定常電流の周りに作られる静磁場のパターン（アンペール・ガウス方程式）と一致すること、そのため②アンペール・ガウス方程式の解であり、電流の磁場を説明するビオ・サバールの法則が、カルタン方程式の解として転位の歪みのパターンにも適用できること、③この性質が図に示す3種類のすべての転位に対して成り立つこと、を示しました。またこれらの結果が、④複素関数論におけるコーシー・リーマン方程式と一致することも示しました。これらの結果から、⑤結晶の欠陥と電磁気学という異なる物理現象が、同じ数学的な原理に基づいていることがわかりました。この背後には、等角写像と呼ばれる機構が深く関わっていることを結論付けました。

本研究成果は、2025年3月5日（水）0時5分（グリニッジ標準時）、日本時間2025年3月5日（水）9時5分に英国王立協会誌「Royal Society Open Science」より公開されました。

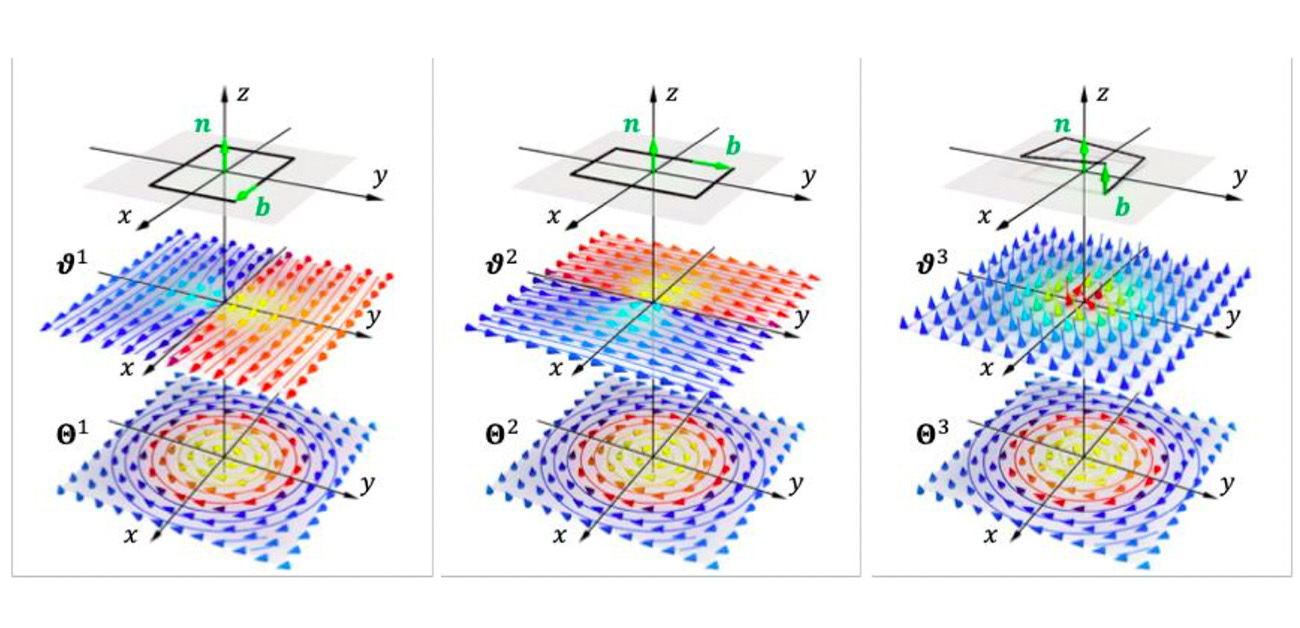
図. 2種類の刃状転位とらせん転位によって生じる結晶格子の歪み場と、そのヘルムホルツ分解の結果。いずれの転位においても、結晶格子の歪み場は全て転位線に沿った右ネジの回転場によって引き起こされており、この物理的な構造は、定常電流の周りに作られる静磁場と、数学的に完全に一致している。そのため転位による歪み場の分布は、電磁気学におけるビオ・サバールの法則を用いて説明することができる。

結晶材料の内部には、「転位」と呼ばれる結晶格子の乱れた領域（トポロジカル格子欠陥）が存在します。個々の転位による結晶格子の乱れは、原子面1層程度のとても小さなものですが、膨大な数の転位が結晶材料の内部で運動・増殖を繰り返すことによって、目に見える大きな塑性変形が発現します。軽量で高い強度を持つ優れた結晶材料を創り出すためには、塑性変形の素過程である転位の性質を理解し、その運動を効果的に制御することが重要です。

そうした結晶材料の設計指針を確立するため、研究グループでは、これまで微分幾何学を用いた転位の理論解析を進めてきました。微分幾何学は、空間の長さや角度を自由に調整することのできる柔らかい幾何学の総称で、私達が暮らすユークリッド空間を数学的に拡張した抽象的な空間を取り扱うための数学です。微分幾何学がもたらす解析空間の飛躍的な拡張は、転位による結晶格子の乱れを表現する上で最適な枠組みを提供します。しかし一方で、数学と材料科学の学際領域研究となることから多くの専門知識が必要となり、これまでほとんど研究が行われてきませんでした。

今回、研究グループが注目したのは転位による塑性変形の方程式です。微分幾何学より導かれる転位の方程式は、カルタンの第一構造方程式（カルタン方程式）と呼ばれています。通常、力学系に関する研究では、現象を記述する方程式は既知の場合が多く、そのため方程式の解の性質を調べ、これを応用へと結び付けることが一般的です。ところが、転位のカルタン方程式はこれまでの研究例が少なく、方程式の基本的な性質が理解されていなかったことから、今回の研究では、カルタン方程式について詳しく調べることから始めました。

研究の出発点となるのは、リーマン・カルタン多様体と呼ばれる曲がった空間上での幾何学です。リーマン・カルタン多様体上では、結晶格子の乱れである転位を、捩率（れいりつ）と呼ばれる幾何構造として数学的に捉えます。今回の研究では、この多様体上で定義されたカルタン方程式とヘルムホルツ分解と組み合わせることによって、転位による塑性変形の核となる方程式を抽出しました。得られた結果は、驚くべきことに、電磁気学でよく知られたアンペール・ガウスの法則と同型となりました（概要①）。中学校の物理学でもお馴染みのこの法則は、定常電流の周りに右ネジ回転の静磁場が作り出されることを記述したもので、その分布は方程式の解であるビオ・サバールの法則に従います。この結果は、単に結晶中の転位と電磁気学の基礎方程式が一致するというだけではなく、電磁気学のビオ・サバールの法則を転位の理論解析へ応用することによって、転位の周りに作られる塑性変形の歪み場を解析的に決定できることを意味しています（概要②）。こうして得られた歪み場の妥当性について検証するため、いくつかの線形近似を用いて問題を簡略化したところ、この理論が導く結果が、これまで知られていた古典的な転位理論の予測と一致することが明らかとなりました。この結果は、微分幾何学を用いた新しい転位論が、ユークリッド幾何学を基盤とした従来の転位論を一般化したことを意味しています（概要③）。

一見すると異なる現象であっても、同じ型の方程式で説明される問題は多数知られています。こうした場合、現象の背後に潜む数学的な共通点を理解することが重要です。そこで今回の研究では、転位の歪み場と電流の静磁場の共通点について一歩踏み込んだ解析を行いました。その結果、複素関数論で用いられるコーシー・リーマン関係式が、両者の共通構造となることが明らかになりました（概要④）。この関係式は、実軸と虚軸を持つ複素平面上の関数解析で用いられる考え方で、複素関数の持つ等角写像と呼ばれる性質を記述することが知られています。この結果は、転位の塑性変形による歪み場が、本質的に結晶格子の角度を保存する性質を持つことを意味しています。この研究成果によって、今後は転位の解析に複素関数論が大きな役割りを果たすことが期待されます。また、アンペール・ガウスの法則はマクスウェル方程式の一部であることから、マクスウェル方程式をより広範に利用した更なる応用解析も期待されます（概要⑤）。

現代社会を支える構造材料の大半は、金属材料（鉄鋼材料やアルミニウム合金など）を中心とした結晶材料によって作られています。結晶材料の強度は転位の力学的な性質によって決まることから、結晶内部で転位の状態を記述するカルタン方程式の理解は、優れた結晶材料の創成を目指す上で極めて重要です。

本研究の成果によって、転位による塑性変形の解析解が見出されたことから、今後は材料強化機構の解明や、ナノテクノロジー分野における微細加工技術など、結晶材料を基礎とした極めて広範な構造材料の設計・解析への応用が期待されます。

本研究成果は、2025年3月5日（水）0時5分（グリニッジ標準時）、日本時間2025年3月5日（水）9時5分に英国王立協会誌「Royal Society Open Science」より公開されました。

タイトル：“Biot-Savart law in geometrical theory of dislocations”
著者名：Shunsuke Kobayashi and Ryuichi Tarumi
ＤＯＩ：https://doi.org/10.1098/rsos.241568

なお、本研究は、科学技術振興機構（JST）戦略的創造研究推進事業さきがけ（課題番号：JPMJPR1997）、および日本学術振興会科学研究費助成事業（課題番号：JP23K13221, 24K00761）の支援を受けて実施されました。

垂水研究室 Webページ
https://nonlinear-solidmechanics.org/