理学研究科 数学専攻 博士課程3年　 安田 順平さん

「4次元空間」と聞いて、どんな空間なのかイメージできるだろうか。答えは「NO」だろう。4次元空間は目に見えない空間だからだ。それは一体どんな空間なのか。どうにかして視認できないか。4次元空間の理解に迫ろうとしているのが、安田さんの研究だ。

計算技術を習得する高校数学とは異なる、大学数学の世界。

安田さんの現在の専攻分野はトポロジー（位相幾何学）。「図形の位置と形相を研究する幾何学」と呼ばれる。「実は、数式を扱うような数学は苦手なんです。それよりもパズルを解いたり絵を描いたりするほうが好き」。そう笑う安田さんにぴったりの学問だ。
大学数学、そして4次元空間に興味を持ったのは高校生の時。数学科出身の先生に、高校までの数学と大学で学ぶ数学は異なり、大学数学は単に計算技術の習得を目指すのではなく、抽象的な概念の理解を深める学問であるということを教わった。大学数学の奥深さに心が躍ると同時に少しの不安も感じたが、「反骨精神じゃないですけど、やってやろうじゃないかと」意志を固めた。そして受験期、図書館で出会った「結び目」の解説本。「変なタイトルだな」と思って何気なく開いたこの本が安田さんの運命を決めることになる。数学と聞いたときにイメージする内容とは全く違う、図形や幾何の世界。その「数学っぽくなさ」に惹かれた。これが、3次元空間、そして4次元空間との出会いとなった。

「曲面結び目」で４次元空間を把握できる？

私たちは３次元空間を生きている。しかし、網膜という「面」を通して物を見る人間は、実は3次元空間すら直接知覚できていない。物体が重なったとき、その重なりの後ろに来る部分が見えなくなることから、「奥行」があることを「認識」している。
そんな3次元空間を単純な図形として表したのが「結び目」だ。曲線や輪っかの交わり方や絡まり方などで空間の奥行きを表現している。結び目の性質や絡まり具合を理解するために、その形を描いたり、ロープや紐を使って結び目を作り、それを解いたり、変形させてみたり。そうした視覚的なアプローチにより、理論的な概念を直感的に理解できる。
すでに3次元空間を「結び目」によって視認できているのだから、同じように図形を視認することで、4次元空間を把握できるのではないか。そうやって、「結び目」を応用して4次元空間を理解しようとする研究が、1920年頃から行われてきた。そこで生み出されたのが「曲面結び目」と呼ばれる理論で、「高さ・幅・奥行き」で構成される3次元空間を表した「結び目」に新しい次元を加えたものだ。安田さんはこの理論を用いて、4次元空間を把握することを試みた。

独自の発想でたどり着いた、「曲面結び目」の表示ツール

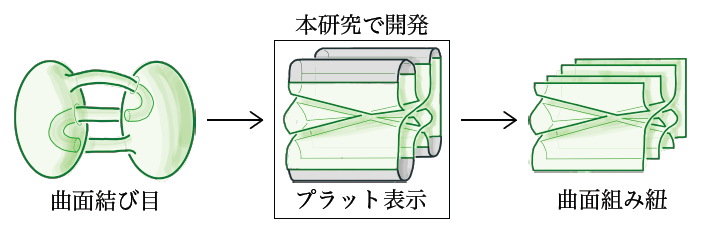
安田さんは、「曲面結び目」を「結び目の時間変形」と解釈。つまり、一つの図形ではなく、時間の流れとともに「結び目」が変化する様子全体を示すことで、4次元空間を把握できないかと考えた。そこで、3次元空間を表した「結び目」に加え、「組み紐（ブレイド）」と呼ばれる垂れ下がる複数の紐を編んでできる図形を抽象化した概念に注目した。ここまでは先行研究でも取り組まれていたが、安田さんはさらに「プラット閉包」という「組み紐（ブレイド）」を「結び目」に変換する手法を応用し、「4次元空間」を表示する新しい「曲面結び目」のパターンを開発した。これは、「4次元空間」を理解する新たな鍵を手にしたといえる快挙だ。この成果は高く評価され、理学研究科優秀研究賞の他、韓国の研究集会においてアワードを受賞。ポーランドのグダニスク大学での講演や研究活動なども行った。「曲面結び目を表示するツールを開発できました。3次元空間の結び目のように、誰が見てもそれが4次元空間を表現していると分かる理論を形作りたい」。謎多き4次元空間がその姿を現す日も近いかもしれない。