東北大学金属材料研究所の芝隼人特任助教（前職：東京大学物性研究所）、山田泰徳元研究員（現職：中国・北京計算科学研究センター）は、名古屋大学大学院理学研究科の川﨑猛史助教、大阪大学大学院基礎工学研究科（前職：新潟大学大学院自然科学研究科）の金鋼准教授と共に、2次元平面内に並んだガラス固体は、結晶性物質と同じしくみで莫大な音波ゆらぎ の増幅が生じることを、大型計算機（スーパーコンピュータ）を用いたシミュレーション計算により世界で初めて見出しました。

ガラス物質は液体のように乱れた原子配列を保ちながら、固体の性質である硬さも伴います。そのため、ガラス物質が示す性質のうち、結晶（規則正しい原子配列を持つ物質）の性質とどこまでが共通し、どこが異なるのか、長い間検討されてきました。中でも分子の動き（ゆらぎ）に関しては、規則的な原子配列の結晶と不規則な原子配列のガラス物質とでは異なるだろうと考えられてきました。しかし、ガラス物質中の分子が実際どのように動くのか、その実態は今でも完全には解明されていません。

本研究は、原子配列に秩序のない物質でも、もともと剛性が低い低次元系は結晶と同様巨大な振動（音波ゆらぎ）が発生するということを示した初めての報告です。本成果は低次元の分子の自由度が主要な役割を果たすソフトマターなどを始めとする材料のゆらぎについて、今まで見過ごされてきた新たな物性を提案するものであり、また広い意味でのガラス物質の今後の物性解明に大きく寄与する成果です。

この成果は米国科学誌「Physical Review Letters」に12月7日にオンライン掲載されました。

ガラス物質は、液体と同じように原子配列が乱れている（非結晶）一方で、固体と同じように硬さを持つことができます。こうしたガラス物質が示す性質は、どこまでが結晶性固体と共通し、どこからが違うのか、百余年の長い間にわたり議論が続けられてきました。ガラスの性質を基礎方程式により解くことは、原子配列に周期性がないという特質から非常に困難です。そのため、コンピュータによるシミュレーション（古典分子動力学法 ）によって、多くの内部自由度を持つガラス形成体の一つひとつを構成する分子の運動を再現し、その性質を明らかにするのが標準的な手法です。

本研究グループの研究ではこの従来の手法に「空間次元による違い」という視点を新たに導入しました。規則正しく原子が並んだ結晶には秩序変数 があるため、平面（2次元面）においては長い空間距離をカバーする大きな音波振動ゆらぎが発生する（Mermin-Wagnerの定理 ）ことが知られています。一方、ガラスにおいては秩序変数がないため、次元によって運動性が変わるということは想定されていませんでした。つまりガラス物質では結晶で見られるような原子のゆらぎは起こらないだろうと考えられていたのです。

本研究グループは、この結晶に見られる大きい空間スケールで発現する音波振動に着目し、ガラス物質でも同じような運動が起こるのではないかと考えました。2次元面のガラス形成体内の分子の動きを確かめるためには多くの分子の数を長い間にわたって計算する必要があります。そこで大型並列計算機（スーパーコンピュータ）を積極的に用いてシミュレーションを行うとともに、短時間から長時間まで広い範囲にわたる大量のデータを効率良く解析しながら研究を進めました。

今回の研究により、本研究グループは大きく3つのことを明らかにしました （図2） 。

まず1つは、上記手法を用いた2次元、3次元のガラス形成体の古典分子動力学計算により、本研究グループは剛性の低い2次元系において特有のゆらぎが見られることを見出しました。さらに2つめの発見として、この2次元系特有のゆらぎを再定式化すると、長いスケールの音波が重ね合わさることにより長さスケールの対数関数に従う振幅の微弱な発散が生じていることを明らかにしました。結果として、2次元のガラス物質でも2次元結晶と同様、熱力学極限で発散する無限大振幅のゆらぎが存在することもわかりました （図3） 。

そして3つめは2次元ガラス形成体には2つの振動運動が存在し、その2つを区別して解析できることを明らかにしました。通常のガラス物質においては構成原子が比較的速く運動する領域、遅く運動する領域が混在しているといわれています（動的不均一性）。たとえば3次元系のガラス形成体にみられる遅い運動の起源となっているのは、粒子がぎゅうぎゅうに詰まることで生じる狭い空間内での振動運動の結果として発生する、間歇的な粒子の入れ替わり運動（ケージジャンプ運動）とされています。3次元でみられるこの振動運動は分子サイズくらいの比較的狭い空間内で通常起こりますが （図4右） 、2次元の場合には振動運動はさらに広い範囲で広がっており、全く運動様式が異なっています （図4左） 。本研究グループは、2次元においてこの巨大な振動運動に隠されるような形で、3次元と同様の粒子の入れ替わり運動が背後で実現している証拠を提示しました。そして、新たな運動変数の導入によって両者の運動を区別して解析できることを示しました。

ガラス物質の動的不均一性については20年余の長くに渡って議論されてきましたが、本研究が示した成果によって、2次元ガラスでは無限大振幅の音波によってさらに速い運動が介在してくることになり、旧来の手法による2次元ガラス形成体の運動の解析は誤りを含んでいることが示されています。本研究では、標準的な解析手法を改め、振動運動を切り離すことによって2次元ガラスの遅い緩和に伴う動的不均一性を抽出する手法を提示しました。

物理の世界では2次元は「低次元」と呼ばれる特別な種類の次元に分類されており、この中では、Mermin-Wagnerの定理に由来する大きい空間スケールにわたる「ゆらぎ」によって特有の物理的性質が発現します。2016年のノーベル物理学賞の主な授与理由のひとつが、トポロジカル相の理論的発見でしたが、これも低次元空間でしか発現しない現象のもっとも際立った例の一つです。このゆらぎは、結晶のように内部に周期構造を持った物質内では生じると報告されていますが、ガラス物質はこのような周期性がないため、長いスケールの波長を持つ音波が示す振舞いは明確に議論されてきませんでした。

ガラスにおける音波振動は原子間の位置関係に直接影響を与えるため、振動が大きくなるということはそれだけ、ガラスが溶けやすく（すなわち「やわらかく」）なっていることを表現しています。本研究グループは、ガラス固体の理論的理解において想定されていなかった音波振動が結晶と同様の振る舞いを見せるということを示しています。すなわち、熱や変形などによって生じるゆらぎが時間の経過につれてどう変化するかに着目すると、もともとの剛性の低い2次元系では長さがスケールアップするほど、徐々に（しかし無限に）振動が強くなっていることが見いだされました （図3） 。言い換えれば、2次元ガラスは巨大になるほどより「やわらかく」なっています。

今回明らかとなった振動の振る舞いは、2次元系内の一層に運動が制約されたコロイド粒子集合体において最もよく実現され、実験的にも諸外国のグループにより実証されつつあり本研究グループの結果は支持されています。原子などの配列が乱れたまま固まる2次元空間のガラス構造は、コロイドや脂質膜・液晶などのソフトマターのみならず、フラストレーションを伴う低次元強相関電子系、例えば有機導体の電荷ガラス状態や超伝導渦系など多様な物質群で作成可能なものであり、今後多様な実験系における観測が期待されます。

雑誌名：Physical Review Letters
英文タイトル：Unveiling dimensionality dependence of glassy dynamics: 2D infinite fluctuation eclipses inherent structural relaxation
全著者：Hayato Shiba, Yasunori Yamada, Takeshi Kawasaki, and Kang Kim
DOI：10.1103/PhysRevLett.117.245701

本研究は文部科学省科学技術人材育成のコンソーシアムの構築事業「計算物質科学人材育成のコンソーシアムの構築事業」（コンソーシアム長：毛利 哲夫東北大学金属材料研究所教授） 、科学研究費補助金・基盤研究(C)「ガラスの多階層ダイナミクスの横断解析―超大規模分子シミュレーション―」（研究代表者：金鋼大阪大学大学院基礎工学研究科准教授）を含む各種研究費の支援を受けて行われました。また、シミュレーション計算には主に東京大学物性研究所スーパーコンピュータ（SGI Altix ICE XA）ならびに自然科学研究機構岡崎共通研究施設・計算科学研究センター（富士通PRIMERGY RX300 S7）を利用しています。

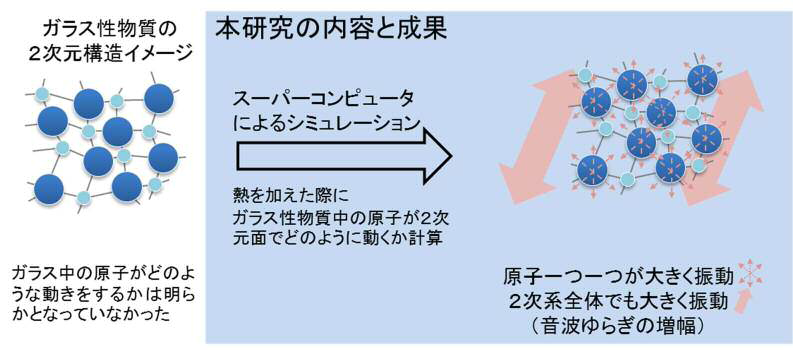
図1　本研究の成果
2次元に並べられたガラス物質は大きな音波ゆらぎを生じる

図2　ガラス物質の各次元で見られる分子の動きの違いと本研究の成果

図3　2次元系の長さと音波ゆらぎの関係
音波ゆらぎの大きさは、2次元系の長さを横軸にとると、対数関数的に無限に増加する。言い換えると、2次元系で長さがスケールアップするほど、熱や変形に対して徐々に（しかし無限に）「やわらかく」なることを示す。

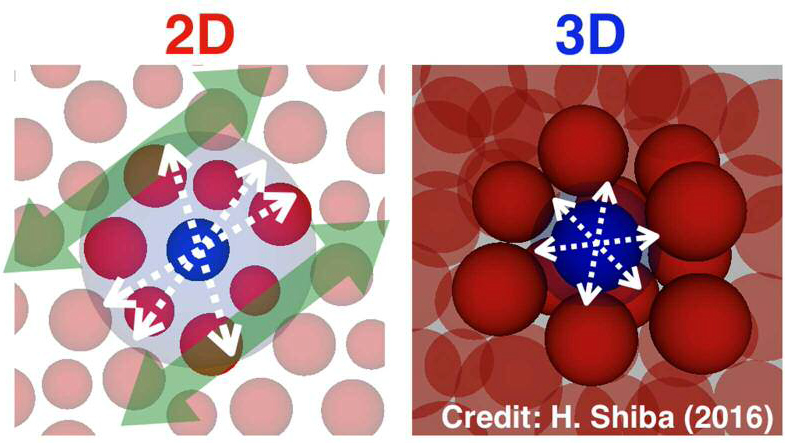
図4　ガラス物質が示す2次元（左）および3次元（右）の粒子配置の模式図
この図では異なる次元間でのガラス固体の運動様式の差を示している。3次元では隣接粒子に閉じ込められた空間内で運動するケージ内により粒子が狭い範囲で振動し、ときどき間歇的に粒子の一つが飛び出し入れ替わることで、遅いダイナミクスが生じる。一方、2次元では、長い波長の音波振動で全体が揺さぶられる運動が発生し、周囲の粒子とともに大きい振幅で振動、水色の丸で示したような大きい範囲で運動することが今回の研究で発見された。しかし、ケージ内より粒子が飛び出すのは3次元系と同様に間歇的である。