コヒーレントX線の斬新な利用法を開発
転位ひずみ場を可視化して、X線渦ビームを発生させる
リリース概要
●コヒーレントX線のブラッグ回折現象を利用して厚い試料のナノスケールひずみ分布を可視化
●ひずみ場の位相特異点を利用した新しい微小X線渦ビーム形成法を提案
大阪大学大学院工学研究科の高橋幸生准教授、理化学研究所播磨研究所放射光科学総合研究センターの石川哲也主任研究員らの研究グループは、物質中の転位ひずみ場を可視化して、X線渦ビームを発生させるというコヒーレントX線の斬新な利用方法を開発しました。
転位とは結晶中に含まれる線状の結晶欠陥のことであり、転位の周りで局所的に結晶はひずんでいます。この転位ひずみ場は、物質の力学特性や電気伝導特性に重要な役割を果たすことが知られています。転位の観察には、X線トポグラフィーや透過電子顕微鏡などが一般的に用いられますが、空間分解能や試料の厚さに制約がありました。研究グループは、大型放射光施設SPring-8 の理研物理科学IビームラインBL29XULにおいて、ブラッグX線タイコグラフィーと呼ばれる方法を開発し、厚さ1マイクロメートルのシリコン中の転位によるひずみ場をナノメートルスケールの空間分解能で可視化することに成功しました。今後、この可視化技術を活用した新しい構造材料や半導体材料の設計・開発が期待されます。
また、研究グループは、シリコン中の転位によるひずみ場を利用することでらせん状の波面をもったX線(X線渦ビーム)を形成可能であることを発見しました。このX線渦ビームは位相特異点と反射面を選ぶことで、軌道角運動量 のモードを制御可能であるという重要な特長を有します。これまで、可視光や電子線を用いた渦ビームの形成については多くの報告がありますが、X線については、ほとんど報告がなく、X線光学の観点からも非常に興味深い結果が得られました。X線渦ビームは強い二色性を示すことが予言されており、物質中の複雑な電子構造の解析への応用が期待されます。
本研究は、日本学術振興会科学研究費補助金の挑戦的萌芽研究「原子分解能X線顕微法の実証と転位イメージングへの応用」(代表者:高橋幸生)の一環として行われました。また、本研究成果は、2013年3月7日(アメリカ東部時間)に米国物理学会誌『Physical Review B Rapid Communications』のオンライン版に掲載されます。
研究の背景
転位とは、結晶中に含まれる線状の結晶欠陥のことであり、転位によってその周囲は局所的にひずむことが知られています。このひずみ場が物質の力学特性や電気伝導特性に重要な役割を果たすことから、転位によるひずみ場の構造を理解し制御することが物質科学における重要な研究課題となっています。転位の観察には、X線トポグラフィーや透過電子顕微鏡が良く用いられます。しかしながら、X線トポグラフィーは空間分解能が数マイクロメートル程度と乏しく、透過電子顕微鏡は試料を数百ナノメートル以下まで薄く加工しなければならないという問題を抱えていました。よって、厚い試料の中の転位ひずみ場を高い空間分解能で観察できるイメージング手法の開発が求められていました。
干渉性の良いX線(コヒーレントX線)を結晶に照射すると、遠方ではブラッグ回折によるスポットに加え、その周囲に結晶内のひずみ場を反映した斑点模様(スペックルパターン)が観測されます。このスペックルパターンに位相回復計算を実行すると、結晶内のひずみ分布を再構成することができます。また、タイコグラフィー(X線照射領域の一部が重なるように試料を走査し、各点からの回折パターンを取得する)を組み合わせることで、大きな結晶試料であってもひずみ分布を得ることが可能です。この方法は特に、ブラッグX線タイコグラフィーと呼ばれています。
本研究グループは、大きくて厚い結晶試料のひずみ分布観察を実現するために、ブラッグX線タイコグラフィーの開発を行い、シリコン単結晶薄膜中の転位ひずみ場の可視化を行いました。
研究成果の内容
実験は、大型放射光施設SPring-8のビームラインBL29XULにて行いました。入射X線エネルギーを11.8keVに合わせ、全反射集光鏡により約1μm(マイクロメートル)のスポットのX線ビームを形成しました。試料には、厚さ1μmのシリコン単結晶薄膜を使用しました。試料を集光点に配置し、(220)結晶面からのコヒーレントブラッグ回折強度をCCDにて測定しました( 図1 )。コヒーレントブラッグ回折強度パターンは、X線照射位置によって大きく変化することが分かりました。転位を横切るようにX線を照射するとX線の破壊的な干渉により、ブラッグスポットは二つに分裂し、特徴的なスペックルパターンが観測されました。また、転位芯にX線を照射すると、ブラッグスポットは同心円に近い形になりました( 図2 )。タイコグラフィー測定によって得られた400枚の回折データに位相回復計算を実行すると、シリコン薄膜中のひずみ分布を反映した試料像が再構成されました( 図3(a) )。観察領域は約10×10μm 2 、ピクセル分解能は約35nm(ナノメートル)でした。再構成された位相像を見ると、部分的に位相が急峻に変化しています。これは、転位によるひずみ場を反映しているものと考えられます。また、位相像には4つの位相特異点があり、二つの微小転位ループの存在が示唆されます( 図3(b) )。研究グループは、この転位による位相特異点にX線集光ビームを照射し、そこから回折したX線は渦ビームとなることを波動光学計算から明らかにしました( 図4 )。このX線渦ビームは、位相特異点の回転方向や反射面を選択することで、軌道角運動量のモードを制御可能なことが分かりました。これまで、可視光や電子線を用いた渦ビームの形成については多くの報告がありますが、X線については、ほとんど報告がなく、X線光学の観点からも非常に興味深い結果が得られました。
今後の展開
今後、物質中のひずみ分布を高い空間分解能で可視化できる今回開発した顕微法を用いた様々な試料観察への応用が期待されます。特に、エピタキシャル薄膜や多結晶体中の結晶粒のひずみ分布観察に有用であり、新しい半導体材料や構造材料の設計・開発につながります。また、転位による位相特異点を利用したX線渦ビームの形成は、まだ、分かっていない点が多く、今後更なる基礎研究が必要です。X線渦ビームは、強い二色性を示すことが予言されており、様々な分光学的な研究に応用できます。たとえば、物質の磁性を根源的に理解できる可能性があります。また、シリコン薄膜はX線吸収が小さく、放射線損傷に対して有利なため、将来、X線自由電子レーザーの渦ビームが形成される可能性があります。
発表論文
“Bragg x-ray ptychography of a silicon crystal: Visualization of the dislocation strain field and the production of a vortex beam”
Yukio Takahashi, Akihiro Suzuki, Shin Furutaku, Kazuto Yamauchi, Yoshiki Kohmura, Tetsuya Ishikawa
Physical Review B (Rapid Communications) 87, 121201 (2013), published online 7 March 2013
参考図

図1 シリコン単結晶薄膜のブラッグX線タイコグラフィーの実験配置
全反射集光鏡によって11.8keVの放射光X線を約1μmのスポットに集光する。集光点にシリコン単結晶薄膜を配置し、(220)結晶面からのコヒーレントブラッグ回折パターンをCCDで測定する。
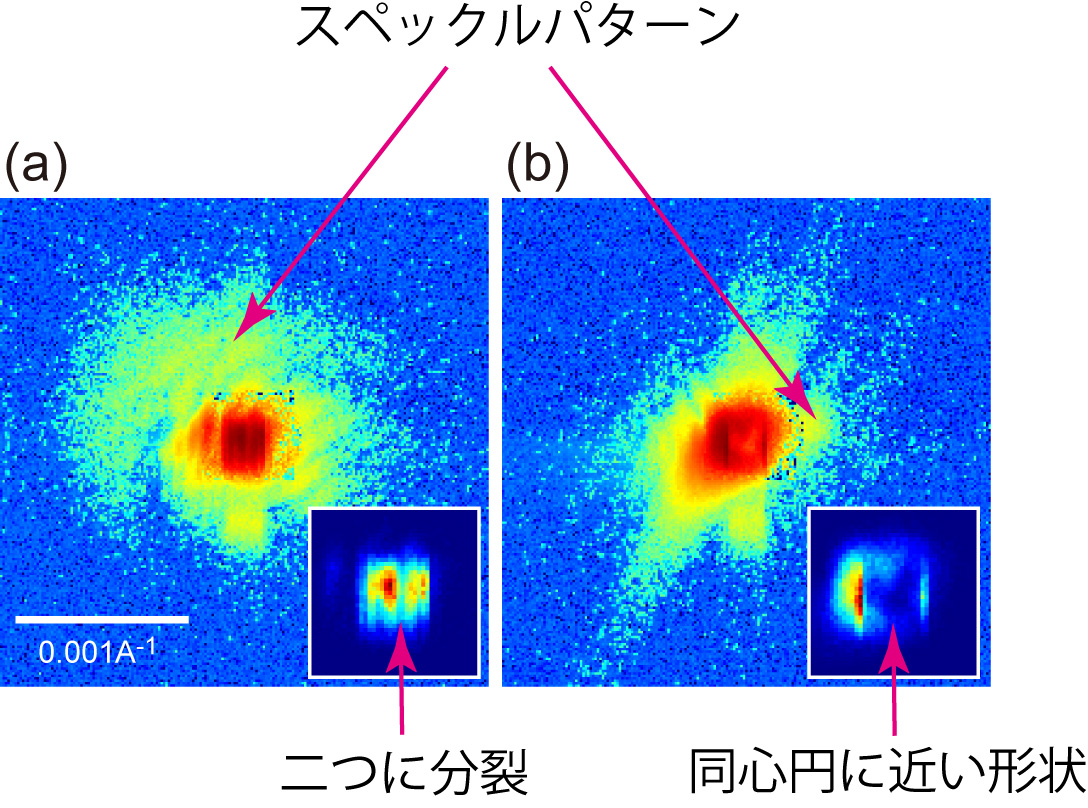
図2 シリコン単結晶薄膜から観測された特徴的なコヒーレントブラッグ回折パターン(対数表示)。右下には、パターンの中心部分を線形表示している。(a)転位を横切るようにX線を照射した場合、(b)転位芯にX線を照射した場合。
シリコン単結晶薄膜にコヒーレントX線を照射すると特徴的なコヒーレントブラッグ回折パターンが観測された。転位を横切るようにX線を照射すると、X線の破壊的な干渉によりブラッグスポットは二つに分裂し、特徴的なスペックルパターンが観測された。また、転位芯にX線を照射すると、ブラッグスポットは同心円に近い形になった。
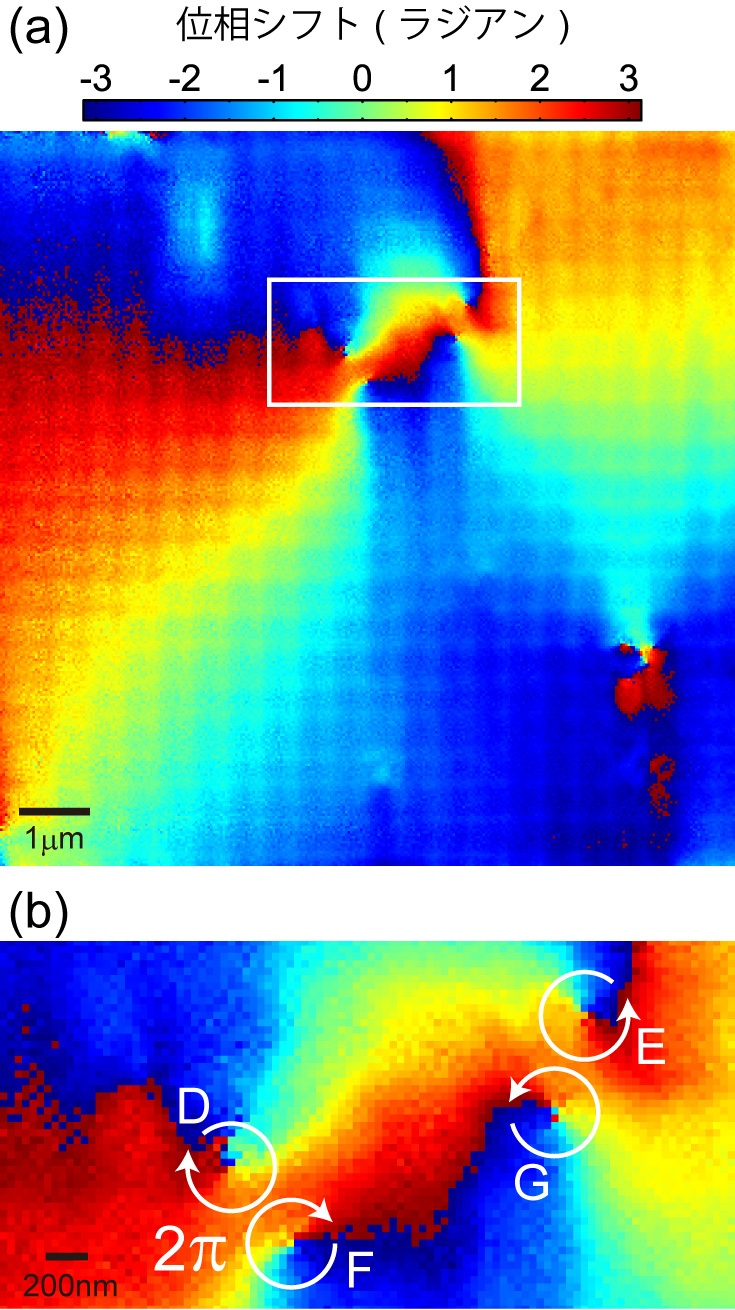
図3 (a)ブラッグX線タイコグラフィーによって得られたシリコン単結晶薄膜の位相シフト像。(b)(a)で四角で囲まれた領域の拡大像。
転位によりひずんでいる領域では位相が急峻に変化している。また、4つの位相特異点が存在しており、その周囲では位相がらせん状に変化している。
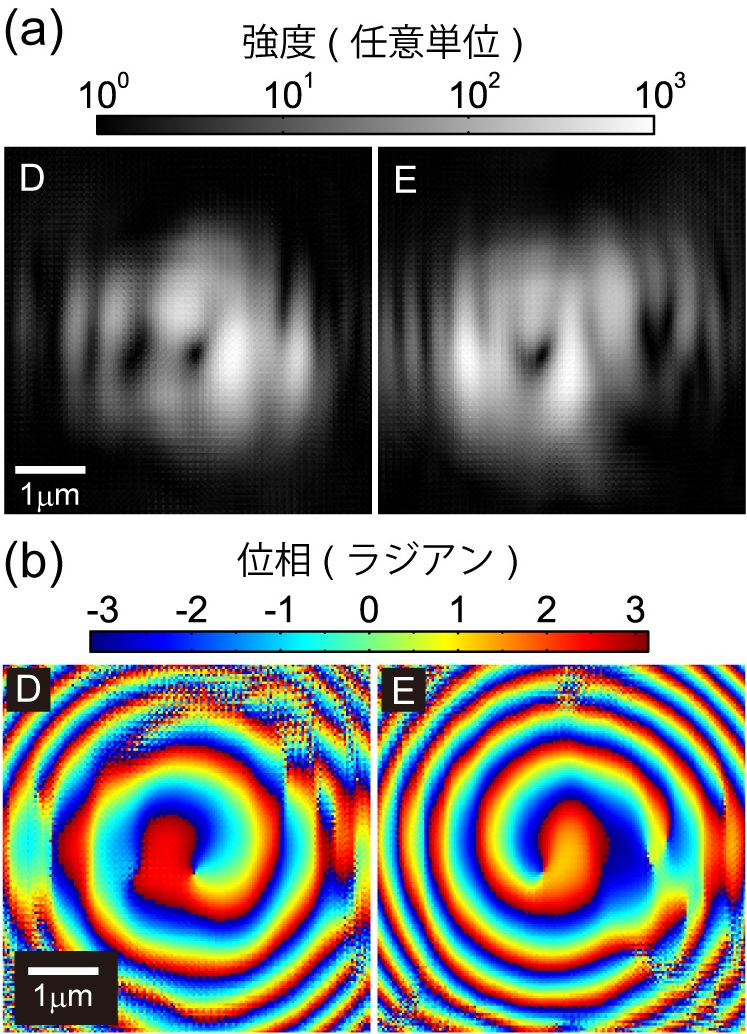
図4 波動光学計算によって得られたX線渦ビームの(a)強度と(b)位相分布。(図3のDとEの位相特異点にそれぞれX線を照射し、試料から10mm伝播した回折波の波動場を計算)
波動光学計算の結果、位相特異点にX線集光ビームを照射することで、X線渦ビームが形成される可能性があることが分かった。位相特異点を選択することで、軌道角運動量のモードを変更できると言える。
参考URL
用語説明
- 大型放射光施設SPring-8
理化学研究所が所有する、兵庫県の播磨科学公園都市にある世界最高輝度の放射光を生み出す共用施設。SPring-8の名前はSuper Photon ring-8 GeVに由来する。放射光(シンクロトロン放射光)とは、荷電粒子が磁場の中で曲がる際に放射される光の一種。SPring-8では、周回する電子群のサイズが小さいことや高い安定性のため、干渉性の優れたX線が得られる。
- 軌道角運動量
位置座標とその共役運動量の外積として表される運動量。原子などの中心力場に束縛された電子にとって、軌道運動量はよい量子数(量子状態を指定する数)となる。
