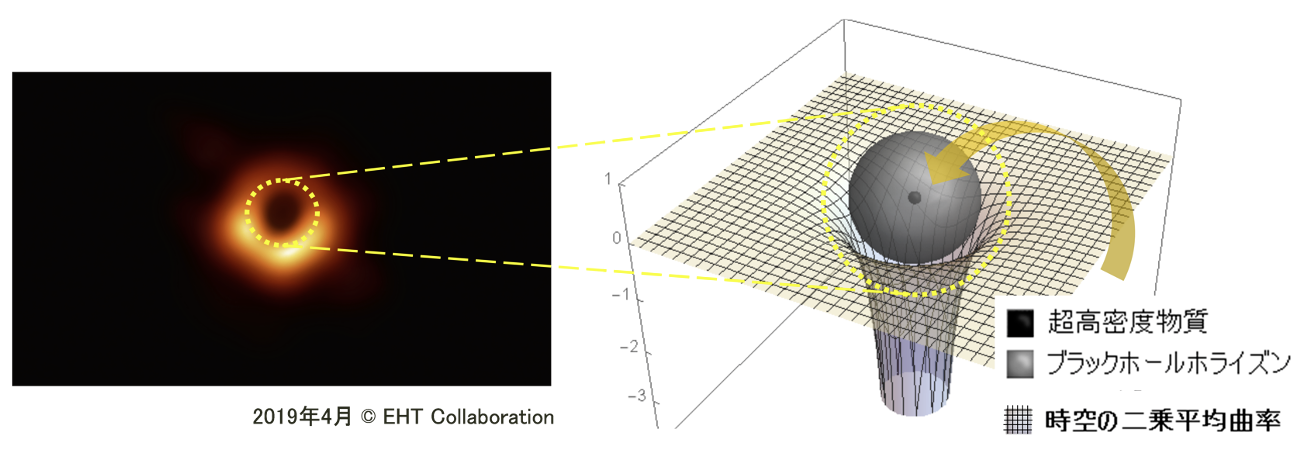
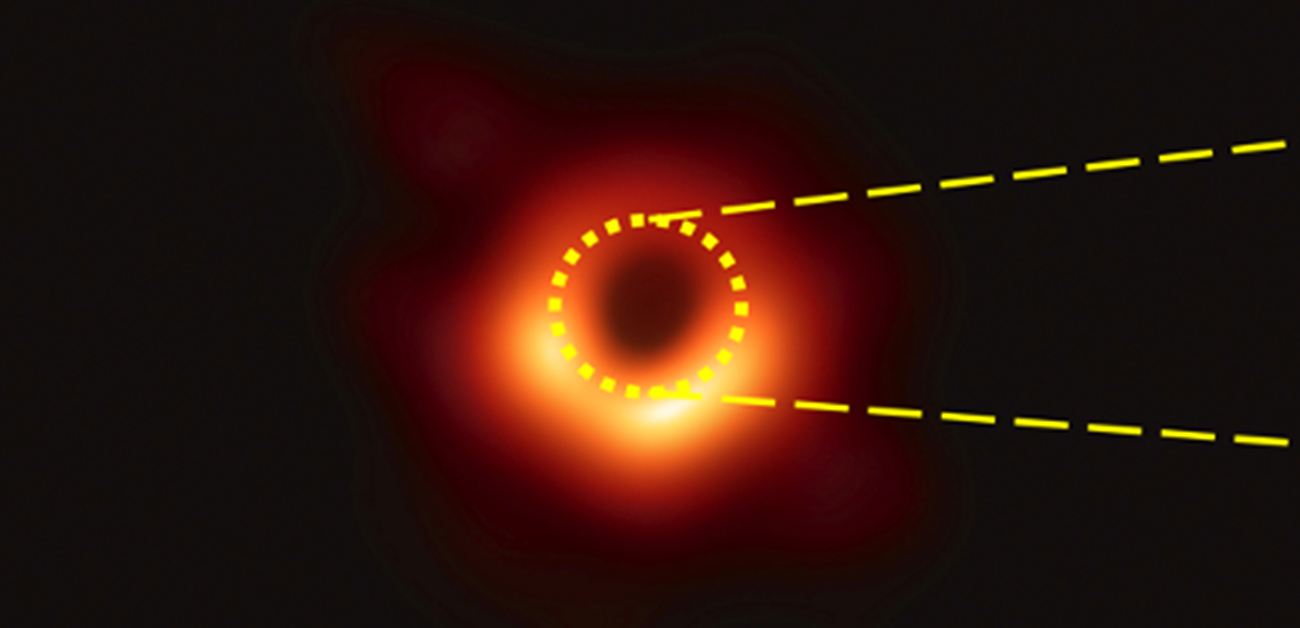
図. （左） M87星雲中の大質量ブラックホール （右）シュワルツシルトブラックホール
ブラックホールの特異点には超高密度物質が存在し、そのエネルギーがブラックホールの質量になる！

アインシュタインの一般相対性理論は、等価原理および一般座標変換を対称性とするゲージ原理と呼ばれる原理を基本として構築された理論です。この理論形式によって物質のエネルギーや運動量が空間の曲がりを決定し、その曲がりが物質の感じる重力となります。このようにエネルギーは一般相対性理論においても中心的な概念ですが、理論の提唱当時からその定義に困難がありました。その理由は、重力と物質との関係を規定するアインシュタイン方程式において、物質のエネルギーと運動量を表すテンソルが通常の保存則を満たさないからです。そこでアインシュタインは重力場に付随するテンソルに似た擬テンソルと呼ばれる量を考案し、これを物質のエネルギー運動量テンソルに付け加えることで保存量を構成できることを指摘しました。そしてこの擬テンソルが重力のエネルギーや運動量を記述するという提案を行いましたが、擬テンソルはテンソルではないため、理論の大事な柱である一般座標変換不変性を満たさず不完全でした。しかしながら、擬テンソルには電磁場のエネルギーの類似物が含まれていることもあり長い間使われ続けました。

その後、様々な議論の結果、曲がった時空におけるエネルギーとして、準局所エネルギーと呼ばれる量やKomar積分と呼ばれる量を状況に応じて計算することが主流になり現在に至ります。準局所エネルギーは、重力場のエネルギーが擬テンソルで表されると仮定すると空間内部に局在するエネルギーが物理的意味をなさなくなることを考慮して時空の十分遠方の表面でエネルギーを計算しようとする考え方で、電磁気学ではガウスの法則を使った全電荷の表面積分による計算に対応します。しかしこれはアインシュタインの擬テンソルの考え方と同様に一般座標不変性を満たしません。その一方、Komar積分は一般座標変換で不変な量でかつどのような時空でも保存するように定義されていますが、平坦時空に適用しても通常のエネルギーに帰着しないため正しいエネルギーとは言えません。

本研究グループの３人は共同で量子重力を研究する過程で複雑に曲がった時空に遭遇し、従来のエネルギーの定義ではこの系のエネルギーを正しく評価できないことを認識しました。そして試行錯誤の末に一般座標変換で不変なエネルギーの定義を見出し、それを最も基本的なブラックホールであるシュワルツシルトブラックホールに適用して既存の結果を再現するか確かめました。すると驚くべきことに、シュワルツシルトブラックホールの特異点には物質のエネルギー運動量テンソルが凝縮していて、それを考慮することで初めて既存の結果を再現する、ということが判明しました。驚くべきである理由は、ブラックホールは伝統的にその内部に物質を何も持たず、「真の特異点」と呼ばれる部分に時空の「穴」だけがあるような天体であるとされてきて、特異点を避けて解析する手法が長い間発展させられてきたからです。この研究によってブラックホール内部にある時空の「穴」は物質がそこに凝縮した結果できたものであり、この寄与を見逃すと一般座標不変なエネルギーの定義を用いて正しい結果を得ることが出来ないということが分かりました。（この物質分布は量子力学ではよく知られた「ディラックのデルタ関数」と呼ばれるもので表され、数学的には「超関数」によって正当化されます。）

さらに進んでこのエネルギーの定義を用いて静止した星のもつエネルギーを計算してみたところ、従来の結果からずれが生じることが判明しました。従来は静止した星のエネルギーは十分遠方における重力場の振る舞いから計算された重力質量と呼ばれるものに一致していましたが、今回私たちが提唱したエネルギーはこの値よりも小さくなることが分かりました。重力質量と値がずれることは一見すると等価原理と矛盾するように思えるかもしれませんが、広がった物体には潮汐力が働くため矛盾はありません。実際に結果のずれを調べると広がった物体の内部における自己重力相互作用を表していることが分かりました。

以上の結果においてブラックホールや星のエネルギーは時間に依存しない保存量ですが、これはネーターの定理の帰結です。そこで「対称性の存在しないような複雑に曲がった時空でも一般座標不変性と矛盾しない形で保存量が存在するのか」というネーターの定理を拡張する問題に挑みました。その結果、宇宙のような全体から成る系においてそのような保存量が存在しその具体的な表示を与えることに成功しました。そしてその結果を私たちが住んでいる宇宙のような系に当てはめると、その保存量をエントロピーと解釈することで熱力学第１法則を満たしていることが分かりました。特に我々の宇宙ではエネルギーは保存しません。またよく知られたブラックホールに対してこの保存量を計算すると、ごく自然な仮定の下に、ベッケンシュタイン・ホーキングの公式から計算されるブラックホールエントロピーと一致することを確認しました。以上のことから、この保存量が一般の閉じた物理系におけるエントロピーではないかと予想しています。

本研究の成果は、一般相対性理論のみならず、より広い枠組みである場の理論に対し新しい視点を与えてくれます。例えば、アインシュタインが付け加えた擬テンソルによる「重力場のエネルギー」は我々が提唱したエネルギーの定義において何ら役割を果たしていませんが、重力がもつとされるエネルギーは一体どうやって観測されるのか、それを考えることは今後の課題です。「２つの星がお互いに回り合う連星は重力波を出すことでエネルギーを失う」と考えられており、「連星の運動中に我々の定義したエネルギーやエントロピーはどのように保存するのか」ということを詳細に調べることは今後の課題であり、我々の見つけた保存量の意味を理解する上での重要なヒントを与えてくれます。その他、今回提唱した保存量は一般の場の理論に対しても存在し計算することが可能であり、流体力学や平衡・非平衡統計物理に応用することで今までとは異なった理解が得られることが期待されます。本研究の成果は、一般相対性理論や一般の場の理論における新しい保存量を通して天文学や宇宙物理学、非平衡統計物理学の理解に大きな影響を与えるだけでなく、量子重力の構築という難問解決へのヒントを与えてくれるかもしれません。

本研究は現代物理学の双璧をなす一般相対性理論と場の量子論の理解に革新をもたらすものであり、そのさらなる応用や実験を含めた既存の結果との比較が重要になってきます。その議論が重力理論の専門家だけに閉じることなく、基礎物理学の研究に関わる多くの研究者によってなされることを期待しています。

＜論文タイトルと著者＞
タイトル：Charge conservation, Entropy Current, and Gravitation (保存則、エントロピー流、そして重力)
著　　者：Sinya Aoki, Tetsuya Onogi, and Shuichi Yokoyama
掲 載 誌：International Journal of Modern Physics A36 (2021), 2150201
DOI：10.1142/S0217751X21502018

＊関連論文
タイトル：Conserved charges in general relativity (一般相対性理論における保存量)
著　　者：Sinya Aoki, Tetsuya Onogi, and Shuichi Yokoyama
掲 載 誌：International Journal of Modern Physics A36 (2021), no. 10, 2150098
DOI：10.1142/S0217751X21500986

本研究は、科学研究費補助金　基盤研究(S)（JP18H05236 代表：初田哲男）、基盤研究(B)（JP16H03978 代表：青木慎也）、基盤研究(C)（JP18K03620 代表：大野木哲也）、基盤研究(C)（JP19K03847 代表：横山修一）の援助を受けています。