制御システムの最適化問題をディープニューラルネットワークで解く
制約付き非線形システムの離散時間確率的最適制御問題への新たなアプローチを構築
概要
情報・システム研究機構 国立情報学研究所(NII、所長:喜連川 優、東京都千代田区)の情報学プリンシプル研究系准教授 岸田 昌子と大阪大学大学院情報科学研究科(研究科長:村田 正幸、大阪府吹田市)の准教授 小蔵 正輝らの研究グループは、一般的に解を求めることが難しいと言われている最適制御問題に対し、制御対象の数理モデルに基づくディープニューラルネットワーク(DNN)を用いて、直感的かつ容易にアプローチする方法を構築しました。この研究は、科学技術振興機構(JST、理事長:濵口 道成、東京都千代田区)の戦略的創造研究推進事業の「CREST AI集約的サイバーフィジカルシステムの形式的解析設計手法(研究代表者:京都大学准教授/NII客員准教授・末永 幸平)」のもとで行われたものです。
非線形システムの最適制御問題は最も汎用的な形の連続最適化問題の一つですが、解析解を求めることは一般的には不可能で、これまでさまざまな数値解法が提案されてきました。しかし、既存のどの方法も非線形システムの最適制御問題の全ての形をカバーすることは難しく、また高度な数学知識が必要となることが大きなハードルとなっていました。
本研究では、特に解くことが難しい、「制約付きの非線形システムに対する離散時間確率的最適制御問題」を解く新たな方法として時相深層展開を提案しています。時相深層展開とは、動的システムの状態変化をディープニューラルネットワークの階層(レイヤー)に展開し、各レイヤーが各時刻での制御入力を決定するパラメーターを持つようにしたものです。このディープニューラルネットワークを訓練することで、適切な制御入力を求めることができるようになりました。本研究成果は、システム科学におけるさまざまな問題に広く適用可能なだけでなく、数学の専門家以外にも使いやすいものであるため、産業界のシステム制御において幅広い活用が期待されます。
本研究成果は、IET Control Theory & Applicationsに2021年11月4日(木)(グリニッジ標準時)に発表されました。
背景
ロボット、自動運転、化学プロセスなどの現実の動的システムの多くは、動作や振る舞いが単純なものではなく重ね合わせの原理が成り立たない非線形システムであり、さらに外部から摩擦や温度変化などランダムな力(確率的な力)の影響を大きく受けています。これらの動的システムを利用する時は、システムが適切な動作をするような制御を行う一方で、制御にかかるコストは抑えなければなりません。このため、さまざまな工学的問題で、「非線形で確率的な動的システムの最適制御問題」が現れてきます。
しかし、この非線形で確率的な動的システムの最適制御問題は、解析的にはもちろんのこと、数値的にも解くことは難しいのが現実です。特に複雑な制約(装置の動作範囲や動作環境など)や非凸関数が含まれる問題では、実用的なアプローチはほとんど知られていません。
研究手法・成果
本研究グループは、「制約付き非線形システムの離散時間確率的最適制御問題」に対し、適切な制御入力を計算するための、直感的かつ容易なアプローチ方法を構築しました。
本技術は、信号処理分野などで近年使われている方法である深層展開の技術に触発され、ディープニューラルネットワークを用いて複雑な動的システムにおける制御入力を計算できるようにしたものです。この技術は、一般的なディープラーニングを用いた手法とは異なり、計算に使うディープニューラルネットワークの構造は元々の動的システムの数理モデルによって決まるのが特徴です。また、制御理論を活用する際にしばしばハードルとなる、非線形な状態変化、非線形な制約、非凸なコスト関数などをそのまま扱うことができ、数理モデルの単純化や技術的な仮定を必要としないという利点があります。
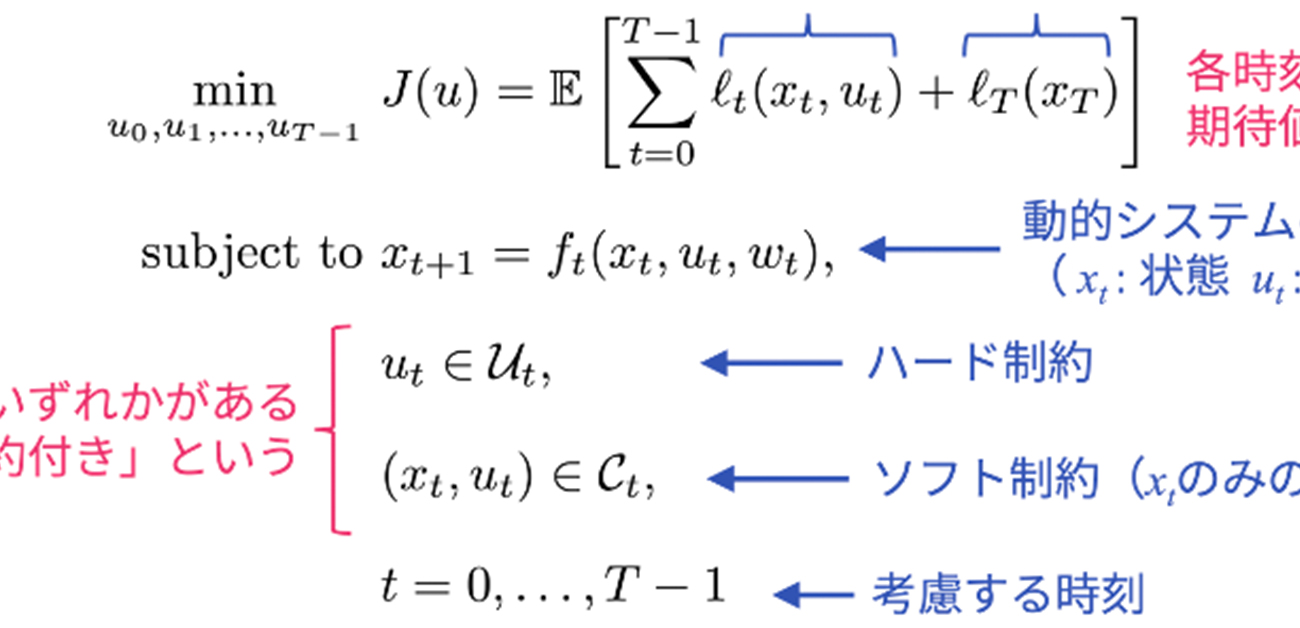
「一般的な離散時間確率的最適制御問題」は<図1>のような数式で表すことができます。また、本研究グループが構築したアプローチで用いるディープニューラルネットワークの構造は<図2>のようになります。

図1. 離散時間確率的最適制御問題
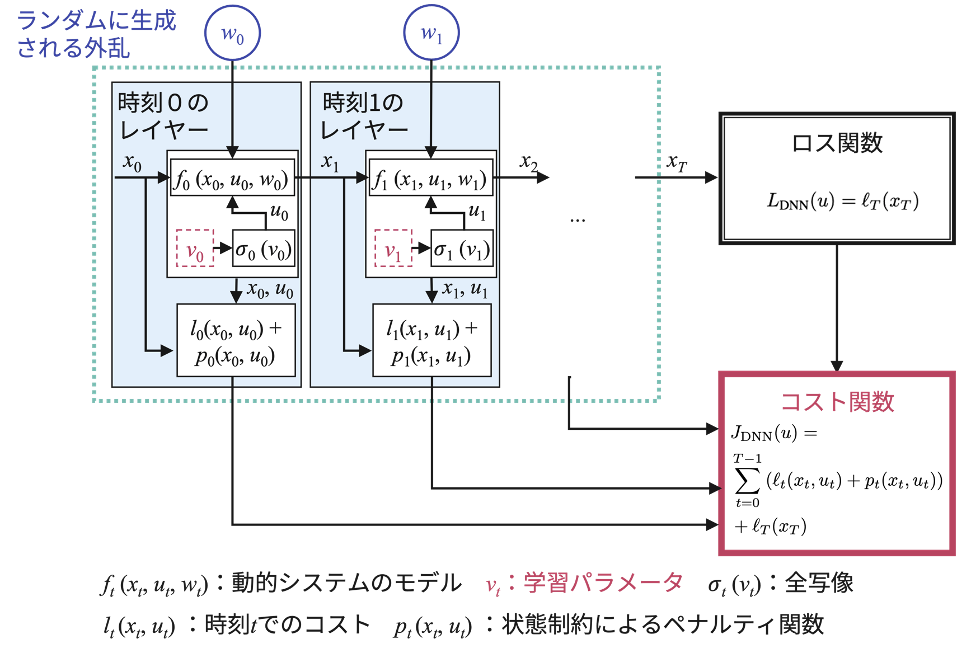
図2. 時相深層展開によるディープニューラルネットワーク(時相深層展開では通常の制御の問題と同様に、動的システムの数理モデルや制約が概ね既知であることが出発点となる)
本研究グループが提案する時相深層展開とは、動的システムの状態変化を多段階のレイヤー構造のディープニューラルネットワークに展開するものです。したがって、各レイヤーはある特定の瞬間における動的システムを表します。また、各レイヤーには、制御入力を決定する学習可能なパラメーターが含まれており、その時点でのランダムに生成された外乱入力を受け取ります。このようにしてディープニューラルネットワークの計算グラフ(計算の全体像)が決まると、標準的な深層学習の手法を用いて、この動的システムの制御入力を決定するパラメーターを学習することができます。
時相深層展開では、制御入力制約(ハード制約)と状態制約(ソフト制約)およびコスト関数の取り扱いが技術的なポイントとなっています。
1. 制御入力制約(ハード制約):
通常、制御信号はアクチュエーター(駆動装置)を動かすことで制御したい対象に入力されるため、その取りうる値に物理的な制約があります。この制御入力の制約は、必ず満たさなければいけないハード制約として考慮しないといけません。時相深層展開において、制御入力制約がない場合は、制御入力をそのまま学習パラメーターとすることが可能ですが、制御入力制約がある場合は、制御入力をそのまま学習パラメーターとすると実際には使えない制御入力が計算されます。そこで、我々は、全写像を使って、学習パラメーターを実行可能な制御入力に移す方法を提案しています。
2. 状態制約(ソフト制約)およびコスト関数:
状態とは動的システムの各時刻の振る舞いを表現するために使われる変数です。状態そのものは必ずしも観測できるとは限りませんが、動的システムの観測できる出力は状態の関数で表されます。状態は外乱に大きく影響されるため、ソフト制約として取り扱うことが普通です。時相深層展開では、通常の最適化問題と同様、ソフト制約はペナルティ関数で表現し、最適化問題のコスト関数に組み込みます。そして、ディープニューラルネットワークを訓練することで、このコスト関数を最小化します。このため、ディープラーニングにおける一般的なロス関数とは異なり、本技術で最小化する関数はディープニューラルネットワークのそれぞれのレイヤーから直接接続されたものになります。
今後の展望
本研究のベースとなるアイデアは、最適化したい変数をできるだけそのままの形でディープニューラルネットワークの学習パラメーターとして埋め込もうというものです。今回論文で取り上げているのは最も一般的な形の制約付き非線形システムの最適化制御問題ですが、時間遅れや不確実なシステムパラメータを含む、より複雑な動的システムへの拡張も容易であると期待できます。
特記事項
【論文タイトルと著者】
タイトル:Temporal Deep Unfolding for Constrained Nonlinear Stochastic Optimal Control
著 者:Masako Kishida, Masaki Ogura (equal contribution)
掲 載 誌:IET Control Theory & Applications
発 表 日:2021年11月4日(木)(グリニッジ標準時)
DOI:https://doi.org/10.1049/cth2.12207
本研究成果は、科学技術振興機構(JST)戦略的創造研究推進事業 CREST「数学・数理科学と情報科学の連携・融合による情報活用基盤の創出と社会課題解決に向けた展開」研究領域(研究総括:上田修功)における研究課題 JPMJCR2012「AI集約的サイバーフィジカルシステムの形式的解析設計手法」(研究代表者:末永幸平)、JSPS科研費21H01352 および大阪大学大学院情報科学研究科スタートアッププログラムの助成を受けたものです。
岸田准教授からのコメント:
「JST CRESTのプロジェクトでは、サイバーフィジカルシステム設計への応用を目標の一つとして掲げています。本成果は機械学習手法として用いられているニューラルネットワークの学習手法をサイバーフィジカルシステムの制御設計において現れる最適化問題の解法に用いるものです。この方法は直感的でわかりやすく、産業界の問題の解決にも大きく貢献できることを期待しています。」
用語説明
- ディープニューラルネットワーク(DNN)
人間の神経回路を模した多層ネットワークであるニューラルネットワークにおいて、ディープラーニングに対応させて4層以上に層を深くしたもの。
- 離散時間
物理系でダイナミクスを記述するのに通常使う微分方程式を、差分方程式で近似したシステムに対して使う時間系。
- 非凸関数
最適化問題において局所的最適解が大域的最適解になるという良い性質をもつ関数。
- 深層展開
信号処理で使われる深層学習の一種で、反復型アルゴリズムの収束を早めるために使われる。
- 全写像
関数fがXからYへの全写像であるときは、Yのどの要素yをとってもXの中のある要素xが存在してf(x)=yとなること。
- ペナルティ関数
制約を満たさない場合に大きな値をとるような関数であり、制約付き最適化問題を制約無し最適化問題に変換するために使われる。
