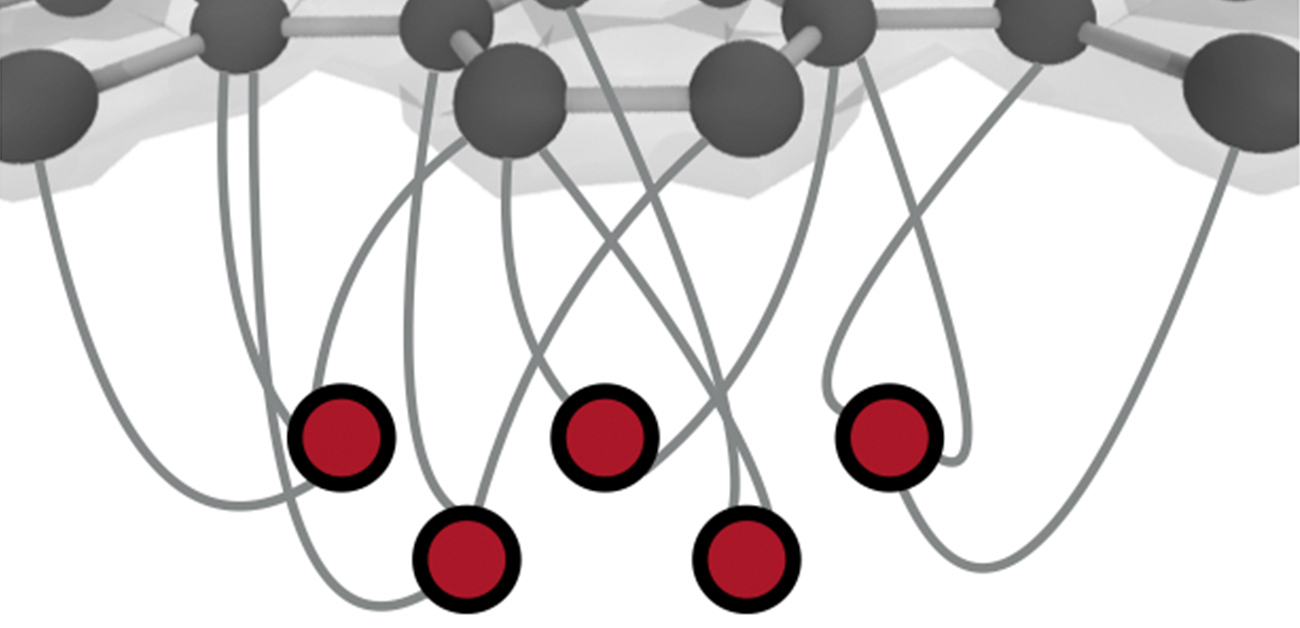
結晶の世界をのぞくニューラルネットワーク
固体系のミクロな量子多体物性に迫る
研究成果のポイント
- ニューラルネットワークを用いて、固体結晶の電子状態の超精密計算手法を新たに開発
- 強相関物質・ポリマー系・無機結晶など既存手法を超える高い汎用性
- 大規模かつ非経験的な化学反応予測・物質設計に向けて大きく前進
概要
理化学研究所(理研)開拓研究本部Nori理論量子物理研究室の吉岡信行客員研究員(東京大学大学院工学系研究科物理工学専攻助教)、フランコ・ノリ主任研究員、大阪大学量子情報・量子生命研究センターの水上渉特任准教授(常勤)の共同研究チームは、機械学習におけるニューラルネットワークの表現能力を応用して、固体系の電子状態に関する第一原理計算を精密に行う手法を提唱しました。
本研究成果は、複雑な電子構造を持つ固体結晶の解析を可能にするだけでなく、物質設計や量子多体 系に関する一般的理解にも貢献すると期待できます。
固体結晶の格子構造や導電性などの性質は、原子を取り巻く電子の状態によって決定されます。ただし、量子力学に従う多数の電子のシミュレーションは難しく、特に電子相関が強い領域において有効な第一原理計算手法は確立されていません。
今回、共同研究グループは、ディープラーニングにおいて強力な非線形関数であるニューラルネットワークが、量子状態でさえも効率的に表現する柔軟性を持つことに着目し、基底状態とバンド構造に関する新たなアルゴリズムを構築しました。この手法は、従来の手法が破綻してしまうほど電子相関が強い物質(水素鎖)や、高速情報処理デバイスの材料となる物質(グラフェン)でも、高精度なシミュレーションが可能です。
本研究は、科学雑誌『Communications Physics』オンライン版(日本時間5月21日午後6時(英国時間5月21日午前10時))に掲載されました。
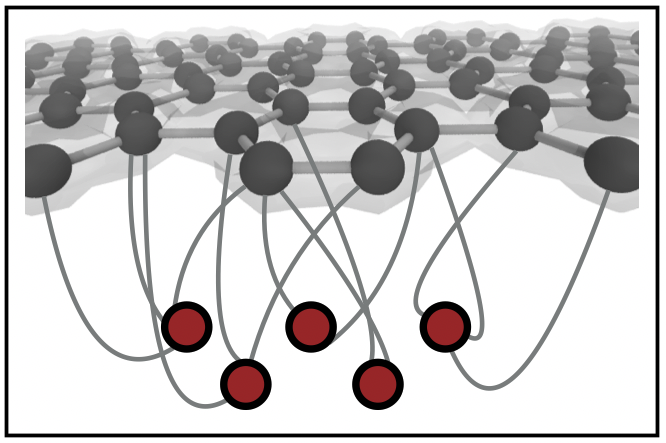
図1. ニューラルネットワークを用いた固体結晶の電子状態の第一原理計算のイメージ。
黒い丸によって表された炭素が六角格子状に連なる、グラフェンの電子状態が、赤い丸で表されたニューラルネットワークにより計算される。
研究の背景
原子が周期的に配列された物質を「結晶(あるいは固体、固体結晶)」と呼びます。結晶は、塩化ナトリウム(食塩)や炭素原子からなるダイヤモンドなどのように、身近に存在します。人工的な雪の結晶作製に世界で初めて成功した中谷宇吉郎博士は、結晶から大気の性質を読み解けることを“天から送られた手紙”と評しました。より広い意味で考えれば、結晶は自然から送られた手紙ともいえ、その性質を調べることは科学者の重要な使命の一つです。
結晶の格子構造や導電性などの性質は、結晶を構成する原子や電子の集団的な振る舞いによって決定されます。原子や電子の運動を量子力学に従う第一原理計算を用いて調べることにより、結晶のさまざまな化学的性質や外場との応答を予測することが可能になります。ただし、膨大な数の粒子を扱う理論やシミュレーション手法はいまだに確立されておらず、極めて困難な「量子多体問題」の一つとして、量子物理学者・量子化学者の前に立ちはだかり続けています。この超難問に対して近年、機械学習におけるニューラルネットワークが強力な武器になるのではないかという見方が強まっています。
本研究の成果
共同研究チームは、固体結晶の性質の中でも特に重要な「基底状態」と「バンド構造」を調べる計算アルゴリズムの開発に焦点を絞りました。
基底状態とは、決められた原子配置に対して、結晶全体のエネルギーを最小化させる電子状態のことです。第一原理計算において、あらゆる電子構造から最も安定な状態を探すには、膨大な計算量が必要です。そこで、電子状態を与える多体波動関数を、ニューラルネットワークによって近似する新手法を提案しました。これにより、ポリマー系から2次元構造の炭素化合物(グラフェン)や無機結晶にいたる広範な物質において、計算量を大幅に削減しつつ、厳密な計算手法に対して「化学精度」と呼ばれる近似精度を達成しました。これは、本手法による計算が、化学反応を予測できるほど精密であることを意味しています。さらに、従来の近似手法では取り扱いの難しい、電子相関の強い領域においても、この手法が有効であることが示されました。
バンド構造とは、固体結晶の電子が持つエネルギーと運動量の関係のことです。レーザー照射への応答や熱・電気的な伝導性などの特性を最も端的に表すため、非常に重要な概念ですが、多体波動関数によるバンド構造は、基底状態のような最適化を通して計算できないため、その計算にはより大きな困難を伴います。一方で、固体結晶中の励起が、電子やプラスの電荷を持つ正孔による1粒子近似によって本質的に規定されていることに着目すると、探索すべき空間を大幅に制限できます。実際に、基底状態を記述するニューラルネットワークから得られる励起部分空間(粒子がとりうる状態が制限された空間)を活用すれば、ポリマー系のバンド構造を計算できることを示しました(図2)。
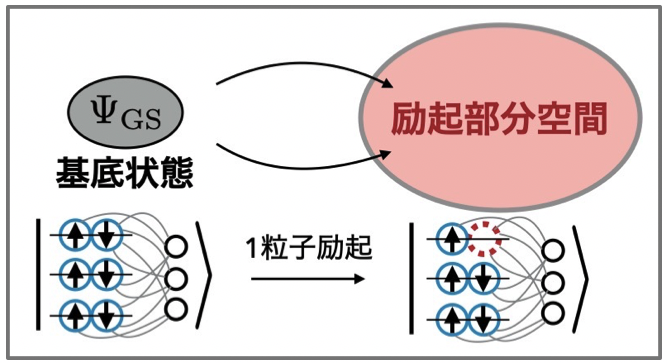
図2. ニューラルネットワークを用いたバンド構造の計算
基底状態を表すニューラルネットワークに対して、電子もしくは正孔を一つ導入する。この「1粒子励起」に必要なエネルギーの大きさから、固体結晶のバンド構造が計算される。図では正孔(赤点線で囲まれた丸)と導入した場合を示している
本研究成果が社会に与える影響(本研究成果の意義)
強い電子相関を第一原理計算で記述する波動関数理論を構築することは、現代の物質科学の根底にある最も大きな課題の一つです。本研究成果は、複雑な電子構造の効率的表現を探究する上で、新たな方向性を開拓したといえ、ニューラルネットワークを用いて量子多体問題に挑むという潮流にさらなる発展を促すものと期待できます。
今後、表面反応をはじめとした従来の第一原理計算手法が破綻するような系にも、本研究の手法が応用されていくことが考えられます。
特記事項
本研究成果は、2021年5月21日(金)午後6時(日本時間)に科学雑誌『Communications Physics』(オンライン)に掲載されました。
タイトル:“Solving Quasiparticle Band Spectra of Real Solids using Neural-Network Quantum States”
著者名:Nobuyuki Yoshioka, Wataru Mizukami, and Franco Nori
なお、本研究は、科学技術振興機構(JST)戦略的創造研究推進事業CREST「超伝導人工原子を使った光子ベースの量子情報処理(領域代表者:蔡兆申)」、文部科学省光・量子飛躍フラッグシッププログラム(Q-LEAP)「量子コンピュータのための高速シミュレーション環境構築と量子ソフトウェア研究の展開(代表者:藤井 啓祐)」、文部科学省光・量子飛躍フラッグシッププログラム(Q-LEAP)「知的量子設計による量子ソフトウェア研究開発と応用(代表者:藤井 啓祐)」、JSTさきがけ「計算化学のフロンティアを拓く革新的複素数波動関数量子シミュレータの開発(研究代表者:水上渉)」、日本学術振興会(JSPS)科学研究費補助金若手研究「Unsold近似を用いた多参照摂動論によるカロテノイド励起状態ダイナミクスの解明(研究代表者:水上渉)」、同基盤研究(A)「Quantum optics in quantum hybrid systems(研究代表者:Franco Nori)」、日本学術振興会国際共同研究事業(JSPS-RFBR)「相互作用を有する空間非一様な二次元構造体(代表者:NORI FRANCO)」、NTT Research「Theoretical studies of topological states in nonlinear optics and synthetic topological matter(代表者:NORI FRANCO)」、Funding Agency Army Research Office(ARO)「Advanced properties of mesoscopic and spatially inhomogeneous electronic matter(代表者:NORI FRANCO)」、Foundational Questions Institute Fund(FQXi)「Exploring the fundamental limits set by thermodynamics in the quantum regime(代表者:NORI FRANCO)」、Asian Office of Aerospace Research and Development (AOARD)「Studies on light-light and light-matter interactions(代表者:NORI FRANCO)」による支援を受けて行われました。
参考URL
水上渉特任准教授(常勤)研究者総覧URL
https://rd.iai.osaka-u.ac.jp/ja/3df5398d10c44be6.html
SDGs目標

用語説明
- ニューラルネットワーク
ニューラルネットワークは、ヒトの脳を模す目的で考案された数理モデル。計算ユニット(ニューロン)を幾重にも連ねたモデルを用いた機械学習は、ディープラーニング(深層学習)として知られる。
- 第一原理計算
経験的なパラメータを含むことなく、量子力学の最も基本的な原理に立脚して電子状態を計算すること。英語ではFirst principles calculationという。
- 量子多体系
量子力学に従って相互作用する多粒子を量子多体系と呼ぶ。
- 電子相関
電子間に働くクーロン相互作用、およびクーロン相互作用による電子の集団的運動への影響。電子相関が強い「強相関物質」では、超伝導や巨大電磁応答などといった、数多くの興味深い現象が発現することが知られている。
- ディープラーニング
ニューラルネットワークの中でも、計算ユニット(ニューロン)を幾重にも連ねたモデルを用いた機械学習は、ディープラーニング(深層学習)として知られる。
- 非線形関数
一次関数(線形関数)では記述できない関数の総称。二次以上の次数を含む多項式や、指数関数などが含まれ、一般に線形関数よりも複雑な振る舞いを示す。
- バンド構造
固体中の電子のエネルギーと運動量の関係のこと。電子の性質ならびに物性を特徴づける物理量である。周期的な構造を持つ結晶性物質では、固体中の電子のエネルギー状態と運動量の関係は、原子間の相互作用によってエネルギー準位間隔は帯状(バンド状)に広がることから、バンド構造と呼ばれる。
- 中谷宇吉郎
1936年に世界で初めて人工雪の製作に成功した日本の物理学者(1900~1962)。『雪』をはじめとした数々の随筆でも知られる。
- 量子多体問題
量子多体系の運動を求める問題を量子多体問題という。
- 多体波動関数
量子多体系のとる状態を表す複素関数。電子の空間分布やエネルギーなど、系を特徴付ける情報が波動関数に埋め込まれている。
- 1粒子近似
量子多体系のとる状態を表す複素関数。電子の空間分布やエネルギーなど、系を特徴付ける情報が波動関数に埋め込まれている。
