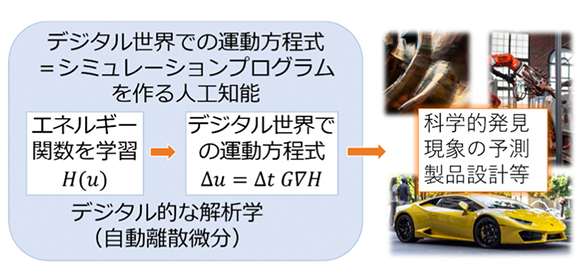
物理法則に忠実なシミュレーションを行う人工知能
デジタル解析学でエネルギー保存・減衰性を再現
概要
神戸大学大学院システム情報学研究科の谷口隆晴准教授、大阪大学大学院基礎工学研究科の松原崇准教授らの研究グループは、人工知能を利用して、詳細なメカニズムや方程式が未解明の現象に対して観測データから物理法則に忠実なモデルを作成し、シミュレーションを行う技術の開発に成功しました。
今後、これまで詳細なメカニズムが不明だったためにシミュレーションが難しかった現象の予測が可能となり、また、シミュレーション自体も高速化されることが期待されます。
この研究成果は、12月7日から開催される、人工知能技術に関するトップ会議であるThirty-fourth Conference on Neural Information Processing Systems (NeurIPS 2020)で発表される予定です。NeurIPS2020投稿論文9454件、採択論文1900件のうち、上位約1.1%、105本のみが該当する“oral”枠で採択されました。
ポイント
・人工知能を活用した物理現象の予測が可能となれば、シミュレーションの高精度化・高速化につながる。
・今までの方法では、デジタル化の影響でエネルギー保存則などの物理法則が成り立たず、予測結果が過大・過小評価になりやすかった。
・本研究では、デジタル的な解析学を活用して、コンピュータの扱えるデジタル世界で物理学を再現し、物理法則を保証しながらシミュレーションを行う人工知能技術を開発した。
・これにより、詳細なメカニズムや方程式が未解明の現象(波の伝搬、亀裂の進展、結晶構造の成長など)であっても、十分な観測データが取得できれば、シミュレーションが可能になると期待される。
研究の背景
通常、物理現象の予測はスーパーコンピュータなどによるシミュレーションによって行われますが、シミュレーションでは、物理学に基づく方程式が使われています。そのような方程式は、汎用性が高い一方で、個々の現象に固有の特徴までを完全に再現することができるとは限りません。例えば、振り子の運動などを高等学校の物理学で学びますが、実際に振り子を作成して揺らしてみると、制作時のちょっとした歪みなどから理論通りに動かないことがあり、シミュレーションの予測に誤差が生じてしまう可能性があります。そこで、近年、現象の観測データを人工知能技術によってシミュレーションに活用する研究が進んでいます。このような方法が完成すれば、実際の現象ごとにオーダーメイドでシミュレーションが可能になり、シミュレーションによる予測精度の向上が期待できます。
しかし、従来の人工知能による予測技術では、コンピュータがデジタル的であるために、現実世界での物理学を取り込むことが難しく、エネルギー保存則などの物理法則を完全に再現することは困難でした。このため、長期間にわたる予測などでは、エネルギーの不自然な増大または減少を伴う可能性がありました。これは、例えば、物体の速さや波の高さなどを過大または過小評価してしまうことにつながり、予測の信頼性に不安を残すものです。
研究の内容
今回の研究では、エネルギーの保存則などを厳密に保ちながら、さまざまな現象の予測を可能にする人工知能技術を新たに開発しました。
新しく開発した方法では「もしも、世界がデジタルだったら」と想定して、そのようなデジタル世界で成り立つべき物理法則を取り入れました。その際、物理法則が微分や積分などといった解析学の言葉で書かれていることに着目し、それをデジタル化した「デジタル解析学」のようなものを活用しています。技術的に説明すると、自動微分による誤差逆伝播法と呼ばれる、人工知能の学習で用いられている技術のデジタル版を新しく開発し、それによってデジタル世界でエネルギー保存則などの物理法則を再現しています。これにより、人工知能技術によるシミュレーションでもエネルギー保存則などを正確に成り立たせることが可能となりました。この方法を用いると、従来の方法で見られたエネルギーの不自然な増大や減少が起こらなくなり、信頼性の高い予測が可能となります。
開発した手法では、人工知能は、物理現象の観測データなどからエネルギー関数を学習し、デジタル世界での運動方程式を作成します。この運動方程式は、そのままシミュレーション用のプログラムとして利用することができ、それを活用した研究開発が可能となると期待されます(図1)。また、コンピュータシミュレーション用に改めて運動方程式を書き換える必要がないため、エネルギー保存則などの物理法則も再現されます。
また、デジタル世界での物理法則を取り込む際には、シンプレクティック幾何学やリーマン幾何学などといった幾何学な視点も使われており、それによって、予測できる現象の幅を大きく広げることが可能となりました。例えば、2つの液滴が近づくと1つになる、といったような現象は、1つになることでエネルギーが減少するということで説明されます。このような現象は、リーマン幾何学を使うとうまく記述できます。実は、幾何学的な観点から見ると、エネルギーが保存する現象も、減衰する現象も、同じような形の方程式で表すことができ、両方のタイプの現象を扱うことが可能な統一的な方法を作ることができます。今回の方法では、そのような考え方を取り入れることで、エネルギーが減衰するタイプの現象についても扱えるように拡張し、エネルギーの減少幅を精度よく見積もることが可能となりました。このような現象の具体例としては、材料の組織形成、結晶成長、亀裂の進展などが知られており、今後、このような現象を予測する人工知能技術の開発が可能になると期待されます。
これに加え、人工知能を学習する際の効率も上がっており、実験では、従来法と比較して10倍程度の高速化が可能となりました。
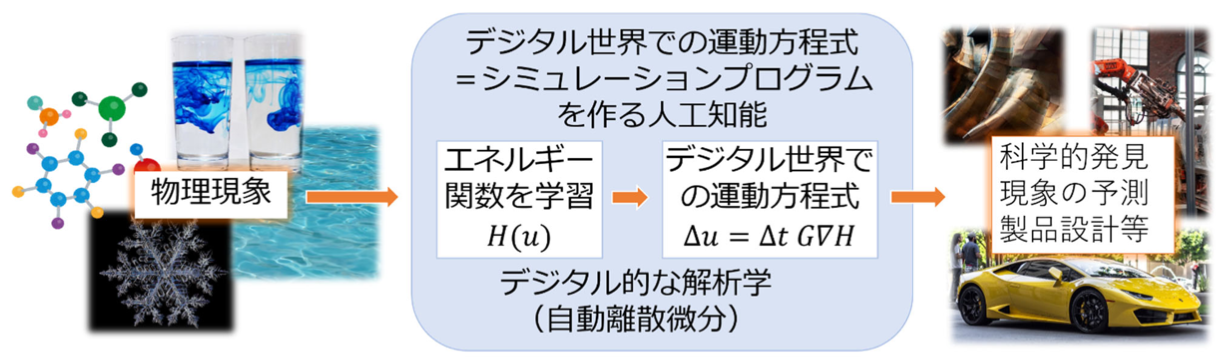
図1 本開発技術の利用イメージ概略
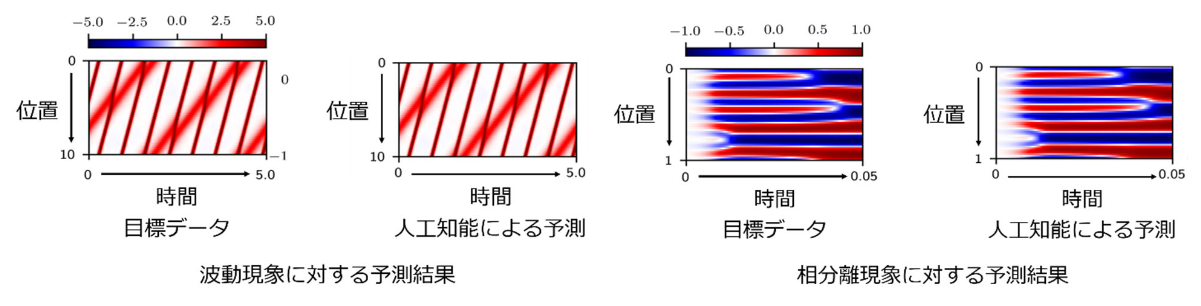
図2 波動現象や相分離現象に対する予測結果 左側は学習の目標となる正解データを、右側は人工知能による予測を表す。目標データに非常に近い予測結果が確認できる。
今後の展開
本研究の技術によって、物理現象の予測の際、人が調整することが難しい、現象の細かい状況を反映したオーターメイドのシミュレーションが可能となり得ます。これは、シミュレーションの精度を向上させると同時に、効率のよい予測が可能となる可能性があり、さまざまな物理シミュレーションの計算速度の高速化にもつながります。
これに加え、詳細が未解明であるためにシミュレーションが困難であった現象も、観測データなどから人工知能によって物理法則を抽出することで、予測可能になる可能性があります。
また、一般に人工知能による予測はブラックボックスと呼ばれることが多く、信頼性が問題になりやすいですが、本手法は、エネルギーの保存則などが忠実に反映されることから、過大または過小な予測が起こりにくく、高い信頼性をもちます。
その他、技術的には、今回の方法は、人工知能の学習で一般に使われている誤差逆伝播法と呼ばれる手法を発展させたものになっています。そのため、今回の技術にかかわらず、さまざまな人工知能の学習を高速化できる可能性があります。
謝辞
本研究は、以下の支援を受けて行われました。
・科学技術振興機構(JST)戦略的創造研究推進事業 チーム型研究(CREST)
研究領域:「数学・数理科学と情報科学の連携・融合による情報活用基盤の創出と社会課題解決に向けた展開」(研究総括:上田修功)
研究課題名:「幾何学的離散力学を核とする構造保存的システムモデリング・シミュレーション基盤」(JPMJCR1914)(研究代表者:谷口隆晴)
・科学技術振興機構(JST)戦略的創造研究推進事業 個人型研究(さきがけ)
研究領域:「社会的課題の解決に向けた数学と諸分野の協働」(研究総括:國府寛司)
研究課題名:「情報幾何学と離散力学の融合と社会ネットワーク解析への応用」(JPMJPR16EC)(研究者:谷口隆晴)
・日本学術振興会(JSPS)科研費
研究課題名:「深層学習に内在する不確実性の利用と制御によるデータ構造理解と異常検知への応用」(19K20344)(研究代表者:松原崇)
・日本学術振興会(JSPS)科研費
研究課題名:「ブラックボックス微分方程式モデルに対する保存則抽出手法とネットワーク解析への応用」(20K11693)(研究代表者:谷口隆晴)
論文情報
・タイトル “Deep Energy-based Modeling of Discrete-Time Physics”
・著者 松原崇1 、石川歩惟2 、谷口隆晴2
1 大阪大学大学院基礎工学研究科
2 神戸大学大学院システム情報学研究科
・掲載誌 Advances in Neural Information Processing Systems 33 (NeurIPS 2020)
参考URL
基礎工学研究科 潮研究室HP
http://ushiolab.sys.es.osaka-u.ac.jp/
用語説明
- 誤差逆伝播法
人工知能を学習するために用いられる技術。人工知能を訓練中に間違えた回答をどのように修正すれば良いかを(計算機に微分を計算させることによって)計算する手法。
- シンプレクティック幾何学
ニュートンの方程式のような力学理論の背景にある幾何学。力学のような物理法則は、特定の座標系に依らずに成り立つと考えられるため、座標系を用いずに記述できると考えられる。シンプレクティック幾何学を利用すると、そのような形で運動方程式を記述・解析することができるようになる。
- リーマン幾何学
長さや角度などの考え方・測り方を一般化して記述できるようにした幾何学。この幾何学の考え方を利用することで、エネルギーが減衰していくような現象を、坂道を下っていく点の動きのようにモデル化することができる。
