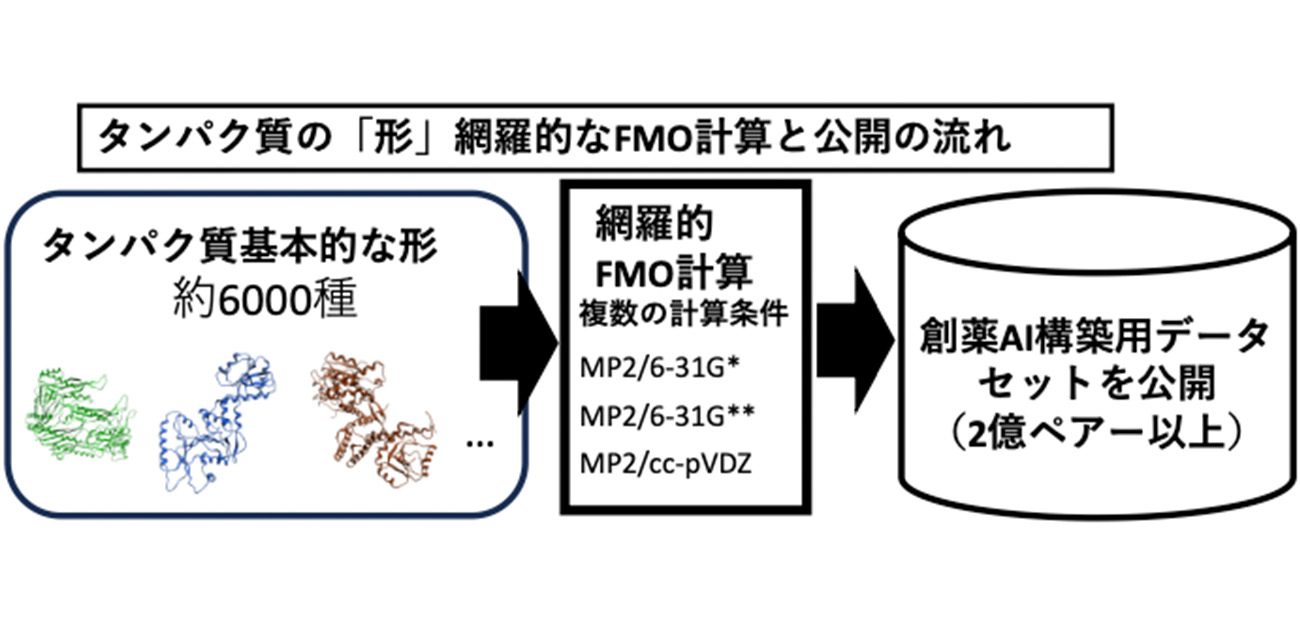
大阪大学大学院薬学研究科の髙谷大輔講師、薬学部の大野修さん、宮岸澄真さん、田中蒼大さん、福澤薫教授らの研究グループは、タンパク質の代表的な「形」を網羅したフラグメント分子軌道（FMO）法による量子化学計算結果のデータセットを世界で初めて公開しました。（図１）

タンパク質や核酸などは、生体内で立体的な構造をしており、その形がそれぞれの分子の働き方を決めています。この形はX線結晶構造解析などの方法で実験的に調べることができます。これまでに2２万以上のタンパク質などの立体的な構造が調べられており、それらのデータはPDB というウェブサイトから、誰でも自由に使えるように公開されています。2024年にノーベル化学賞を受賞したAlphaFold2は、AI技術により、タンパク質の立体的な構造を計算科学的に高い精度で予測できるようになり、タンパク質の設計に大きな革新をもたらしましたが、このAIもPDBのデータを学習しています。つまり、もっと多くのデータがあれば、より良い予測ができるようになります。またタンパク質の形以外のデータが役にたつ可能性もあります。これからも新しいAI技術を進化させるためには、こういった実験データと計算データを集めて共有することが大切になってきます。

研究グループでは、タンパク質の機能には、その形状以外に構造に基づく分子内・分子間の相互作用も重要であると考え、分子の電子状態に基づいた相互作用の正確な理解と創薬への応用を目指しています。そこでフラグメント分子軌道 (FMO) 法 という量子化学計算手法 の1つを用いて、SCOP2分類というPDBに登録されている約6000構造もの基本的な形（フォールド）の代表に対して網羅的な計算を実施して、相互作用のデータを取得しました。FMO計算では、いくつかの異なる計算レベルを使いました。たとえば、6-31G*, 6-31G**, cc-pVDZという基底関数を使って電子相関を含むMP2レベルの計算をしています。この計算によって、約 6000のタンパク質の構造を調べ、その中で2億以上のアミノ酸残基ペアの間でどのような相互作用が働いているかを定量的に解析しました。具体的には、静電相互作用や分散相互作用などのエネルギーを計算して、それぞれの強さを明らかにしています。本研究で提供する相互作用データは、タンパク質の電子状態に基づく機能解析およびAI構築などの機械学習の役にたつと期待されます。

本研究成果は、米国科学誌「Scientific Data」に、10月23日（１０PM日本時間）に公開されました。またデータはhttps://doi.org/10.6084/m9.figshare.25980112.v2から、誰でも自由にダウンロードできます。(ライセンス:CC-BY-4.0)

図1. 量子化学的な相互作用のデータにより創薬AI構築を加速させる！

近年、予測精度のよいAIを構築するために大量のデータが必要になってきています。例えばタンパク質の立体構造を予測するAIであるAlphaFold2などもPDBなどに登録されているタンパク質などの立体構造の公開データを学習しています。つまり、もっと多くのそして多様なデータがあれば、より良い予測ができる可能性が高まります。実験データ以外にもシミュレーションによるデータも有効に利用できるデータとして注目されています。これからも新しいAI技術を進化させるためには、こういった実験データと計算データを集めて共有することが大切になってきます。

本研究では、創薬に関連するタンパク質などの生体高分子について様々な観点からの計算データセットの提供を目的にしており、タンパク質の代表的な「形」（フォールド）を網羅したFMO法による量子化学計算結果のデータセットを作成し、自由に使えるライセンスのもとで公開することを目指しました。

タンパク質や核酸などの生体高分子の３次元構造はその機能を表すとされており、X線結晶構造解析、NMR及びクライオ電磁顕微鏡等の実験手法によりその構造を決定することが可能です。構造生物学コミュニティのデータ蓄積の成果によって、現時点で2２万以上の構造がPDBのウェブサイトから公開されており、その数は年々増加しています。（図２）

計算科学では、これらの構造データを用いた分子シミュレーションにより、「形」だけでなく、さまざまなデータを提供することが可能です。例えば、タンパク質は分子の一種であり、電子の偏りによって正および負の極性を持つため、その電子状態を正確に求めることが機能解明において重要となります。量子力学(Quantum Mechanics; QM) にもとづく量子化学計算は、分子が持つ電子の状態を計算する手法で、酵素などの化学反応や分子認識の解析に使用されてきました。一般的に量子化学計算を生体高分子に適用するには計算コストなど様々な課題があり、日本発のフラグメント分子軌道 (FMO)法は、現時点において生体高分子に対して適用可能な最先端のQM計算手法として提案されています。FMO法ではタンパク質のような生体高分子をアミノ酸などの残基単位のフラグメントに分割し、計算を実行します。

FMO法により得られるデータはフラグメント間相互作用エネルギー(Inter-Fragment Interaction Energy; IFIEまたはPair Interaction Energy; PIE)があり、このIFIEはPIEDA (Pair Interaction Energy Decomposition Analysis)より、静電相互作用(ES)、交換反発項(EX)、電荷移動項(CT+mix)、分散相互作用(DI)の４つの成分に分解する事で、これらのどの成分がフラグメント間の結合に強くかかわっているかを定量的に知ることができます。（図３）例えばアミノ酸の主鎖及び 側鎖に頻出する水素結合が強い場合はESとCT成分のエネルギーが強く表れ、バリンやトリプトファンやフェニルアラニンが関与するメチル基と芳香環などの相互作用には主に非極性の相互作用の評価に適したDI成分が現れます。これらの結合は生体高分子の相互作用によくあらわれ、タンパク質分子の特徴を表す記述子としても使用する事が期待されています。また創薬においてはタンパク質とリガンド分子の相互作用評価が重要であるため、PIEDAによる相互作用の特徴づけは、定性的もしくは定量的な相互作用の解析においても使用されます。

本研究グループではSCOP2分類というPDBに登録されている約6000の基本的なフォールドの代表（図4）に対し、網羅的にFMO計算を実施して、電子状態に基づく残基間相互作用のデータを取得しました。量子化学計算はABINIT-MPプログラムを使用し、網羅的な計算は大阪大学D3センターの大型計算機「SQUID」を用いて実施されました。

また本研究のFMO計算データはいくつかの異なる計算レベルを用いて、それぞれの計算を行いました。Møller-plessetの２次摂動を用いたMP2法を用いて、6-31G*, 6-31G**, cc-pVDZという３種類の基底関数を使って計算しています。この計算では約6000のタンパク質の構造を調べ、その中で2億以上のアミノ酸残基ペアの間でどのような相互作用が働いているかを調べました。

図5ではその解析例の１つであるFMO-MP2/6-31G*レベルにおける20種の天然アミノ酸（タンパク質を構成する基本フラグメント単位）間の相互作用を紹介します。この解析により、PIEDAエネルギー成分のヒートマップでは、アミノ酸残基のすべての組み合わせについて、相互作用エネルギーが計算されています。まず、ESエネルギーは比較的わかりやすく、正（プラス）と負（マイナス）の電荷を持つアミノ酸同士は引きつけ合い、逆に、同じ符号の電荷を持つアミノ酸同士は反発し合います。一方、DIのエネルギーでは、主に疎水性（つまり水をはじく）アミノ酸残基同士の間に多くの分散相互作用が見られました。本研究では他の２つの基底関数、つまり6-31G**, cc-pVDZを用いた結果についても比較検討されています。

図2. 本研究では多様なタンパク質のフォールドに対する量子化学的データの提供を目的とする

図3. FMO法によるPIEDAの各成分と代表的な相互作用の分類

図4. 本研究の計算対象である代表的なタンパク質の例
6000弱の多様なFMO計算前タンパク質構造(SCOP 2.0[4]より抜粋）

図5. 本研究で得られたデータの解析事例：FMO-MP2/6-31G*計算条件における20種のアミノ酸の相互作用の中央値のヒートマップ

本研究成果により提供されるタンパク質の代表構造網羅的な量子化学計算と相互作用解析によって、タンパク質の基本構造を理解することができ、またこれらのデータを学習したAIの構築による創薬等への応用が期待されます。このような複数の観点から比較可能なデータセットは基礎研究を加速させることが期待されます。

本研究成果は、2024年10月23日（１０PM日本時間）に米国科学誌「Scientific Data」（オンライン）に掲載されました。

タイトル：“Quantum chemical calculation dataset for representative protein folds by the fragment molecular orbital method”
著者名：Daisuke Takaya, Shu Ohno, Toma Miyagishi, Sota Tanaka, Koji Okuwaki, Chiduru Watanabe, Koichiro Kato, Yu-Shi Tian, Kaori Fukuzawa
ＤＯＩ：https://doi.org/10.1038/s41597-024-03999-2

本成果の一部は国立研究開発法人日本医療研究開発機構(AMED) 生命科学・創薬研究支援基盤事業（BINDS）の支援（課題番号: JP23ama121030）、および大阪大学D3メディアセンターのSQUID(課題番号: hp240114)を使用されました。またFMO創薬コンソーシアム( FMODD）の活動の一環として、富岳スーパーコンピューター（プロジェクトID: hp240162）を使用されました。 また本研究の一部はJSPS科研費 23K11320の助成を受けたものです。

福澤薫教授 研究者総覧
https://rd.iai.osaka-u.ac.jp/ja/ad43782126285f59.html

髙谷大輔講師
https://rd.iai.osaka-u.ac.jp/ja/fe24884432776b42.html?k=髙谷