この研究についてひとこと
光の優れた計算能力を活用した空間光イジングマシンに対して、ちょっとした数理的なアイデアを加えることで、世界が大きく拡がりました。物理・数理・情報の異分野融合の魅力がよく表れた研究成果だと考えています。今後も空間光イジングマシンの実応用に向けて研究を展開していきたいと思います。
鈴木秀幸
- 情報科学研究科
- 教授
光による組合せ最適化と統計的学習の新計算モデル
大規模な実問題を解く空間光イジングマシンの実現に道筋
研究成果のポイント
概要
大阪大学大学院情報科学研究科の鈴木秀幸教授および谷田純教授らの研究グループは、光を用いて組合せ最適化問題を解く空間光イジングマシンの適用範囲を飛躍的に拡大する、新しい計算モデルを提案しました。
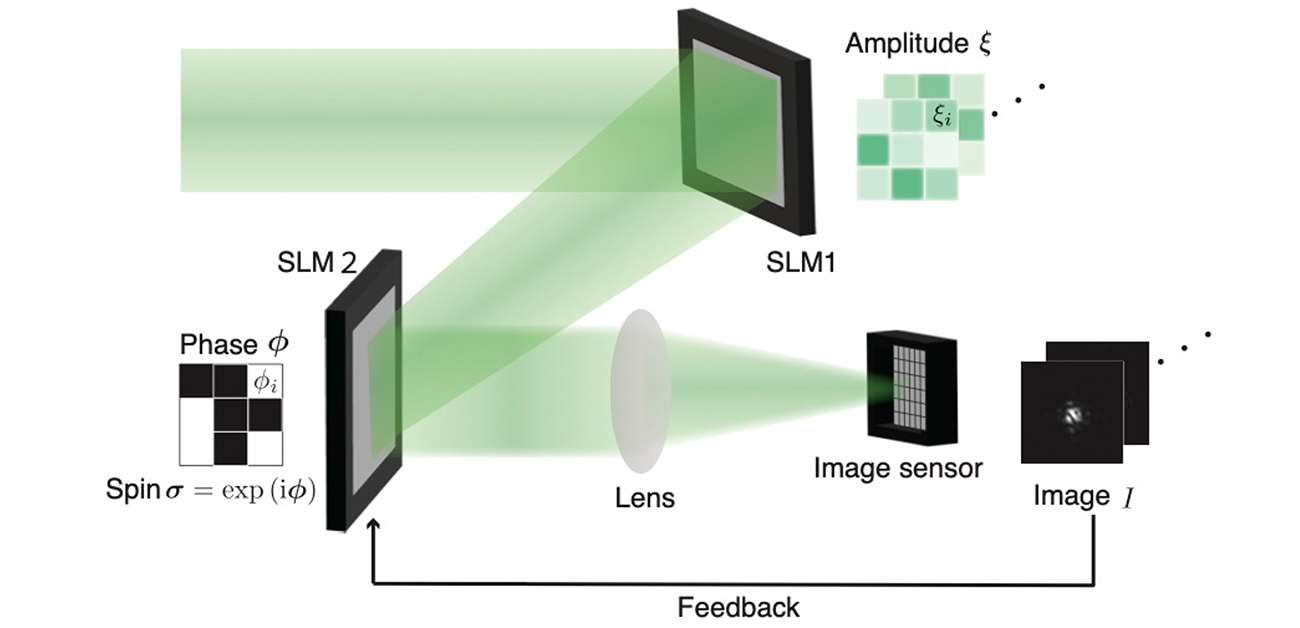
空間光イジングマシンは、光の並列性を活用することにより1万変数以上の大規模な組合せ最適化問題を高速・高効率に扱うことができるという優れた特徴を持ちます（図1）。しかし、これまでは扱える問題に厳しい制約があり、実問題への応用において大きな課題となっていました。
今回、研究グループは、この課題を解決し、空間光イジングマシンが扱える組合せ最適化問題の範囲を飛躍的に拡大する計算モデルを提案しました。この計算モデルを用いると、光の特性により大規模で全結合のイジング問題が効率的に扱えるだけでなく、特に低ランク性を持つ問題に対して高効率であるという独自の特徴を持つことが明らかになりました。また、この計算モデルが組合せ最適化だけでなく統計的学習にも適用できることを示しました。これらの研究成果は、大規模な組合せ最適化と統計的学習の実問題を解く新しい光計算技術の実現に道筋を付けるものであり、計算の高速・高効率化だけでなく、社会課題への応用を通してエネルギー利用の効率化やカーボンニュートラル実現への貢献等も期待されます。
本研究成果は、米国物理学会の速報論文誌「Physical Review Letters」に8月7日（月）（米国東部時間）に掲載されました。
図1. 空間光イジングマシンの概略図。1万変数以上の大規模な組合せ最適化問題を扱うことができる。光の空間並列性により、変数の数が増えても計算の1反復にかかる時間はほとんど増えることがない。
研究の背景
イジングマシンとは、イジング問題と呼ばれる組合せ最適化問題を高速に解く専用ハードウェアです。多くの重要な組合せ最適化問題がイジング問題として表現できることから、量子アニーリング等の様々な原理に基づくイジングマシンの研究開発が盛んに行われています。
2019年に提案された空間光イジングマシンは、空間光変調を用いて組合せ最適化問題を解くイジングマシンです。光の空間並列性を活用することにより、計算の1反復にかかる時間が原理的には変数の数によらず一定となり、1万変数以上の大規模なイジング問題であっても高速・高効率に扱えることから、優れたスケーラビリティを持つイジングマシンとして期待されています。また、光を用いるため結線が不要であり、全結合の問題が容易に扱えることも優れた特徴です。しかし、これまでは扱えるイジング問題に厳しい制約があり、実問題への応用において大きな課題となっていました。
研究の内容
研究グループは、空間光イジングマシンのハードウェア実装を変えることなく、任意のイジング問題を扱うことができる新しい計算モデルを提案しました。この計算モデルを用いると、光の特性により大規模で全結合のイジング問題が効率的に扱えるだけでなく、特に低ランク性を持つイジング問題に対して高効率であるという独自の特徴を持つことが明らかになりました。実際に、これまで空間光イジングマシンが扱えなかった整数重みナップサック問題を低ランクのイジング問題として定式化し、最適化計算が可能であることを実証しました。また、この計算モデルにより統計的学習を行うための具体的な学習則を導出し、手書き数字画像データの低ランク学習が行えることを示しました。これらの研究成果は、大規模・全結合・低ランクの性質を持つ組合せ最適化と統計的学習の実問題に対して特に優れた性能を持つ空間光イジングマシンの実応用への道筋を示すものです。
本研究成果が社会に与える影響(本研究成果の意義)
この計算モデルにより空間光イジングマシンの実応用が進展すれば、大規模な組合せ最適化と統計的学習の実問題に対する計算の高速化や消費電力の低減が期待されます。また、複雑化・大規模化する社会課題への応用が進展すれば、社会システムのさらなるスマート化、たとえばエネルギー利用の効率化やCO2排出量の低減によるカーボンニュートラル実現への貢献等も期待されます。
特記事項
本研究成果は、大阪大学大学院情報科学研究科情報数理学専攻において、非線形数理講座の鈴木秀幸教授、山下洋史助教、大久保健一特任助教（常勤）（現在は山口東京理科大学助教）と、情報フォトニクス講座の谷田純教授、小倉裕介准教授、下村優助教との共同研究により得られたものです。2023年8月7日（米国東部時間）に米国物理学会の速報論文誌「Physical Review Letters」（オンライン）に掲載されました。
タイトル：“Low-rank combinatorial optimization and statistical learning by spatial photonic Ising machine”
著者名：Hiroshi Yamashita, Ken-ichi Okubo, Suguru Shimomura, Yusuke Ogura, Jun Tanida, and Hideyuki Suzuki
ＤＯＩ：https://doi.org/10.1103/PhysRevLett.131.063801
なお、本研究は、科学技術振興機構（JST）戦略的創造研究推進事業CREST「Society 5.0を支える革新的コンピューティング技術」研究領域（研究総括：坂井修一）における研究課題「光ニューラルネットワークの時空間ダイナミクスに基づく計算基盤技術」（研究代表者：鈴木秀幸、課題番号：JPMJCR18K2）等の一環として行われました。
参考URL
SDGsの目標
用語説明
- 組合せ最適化問題
様々な選択肢の組合せの中から最も良いものを見つける問題のことを言います。選択肢を表す変数が増えると、考慮すべき組合せが急激に増えてしまいます。そのため、大規模な組合せ最適化問題を解くためには計算の効率化や高速化が求められます。
- イジングマシン
イジングモデルとは、スピンと呼ばれる±1の2値を取る変数が相互作用する数理モデルの一つです。イジング問題とはイジングモデルのエネルギーを最小化する問題のことで、これを高速に解くための専用ハードウェアがイジングマシンです。多くの重要な組合せ最適化問題がイジング問題として表現できることが知られています。大規模とは変数の数が多いこと、全結合とは任意の2変数間の相互作用を許すことを意味します。
- 低ランク性
行列が低ランクとは、小さい行列の積として表現できることを意味します。本研究では、イジング問題における変数間の相互作用を表す行列が低ランクであることを、イジング問題の低ランク性と表現しています。一般に現実のデータは低ランク行列によって良く説明できる構造を持つと想定されます。そのため、低ランク性を持つ問題に対して高効率という、本研究で明らかになった空間光イジングマシン独自の特徴は、広く有用なものであると期待されます。
