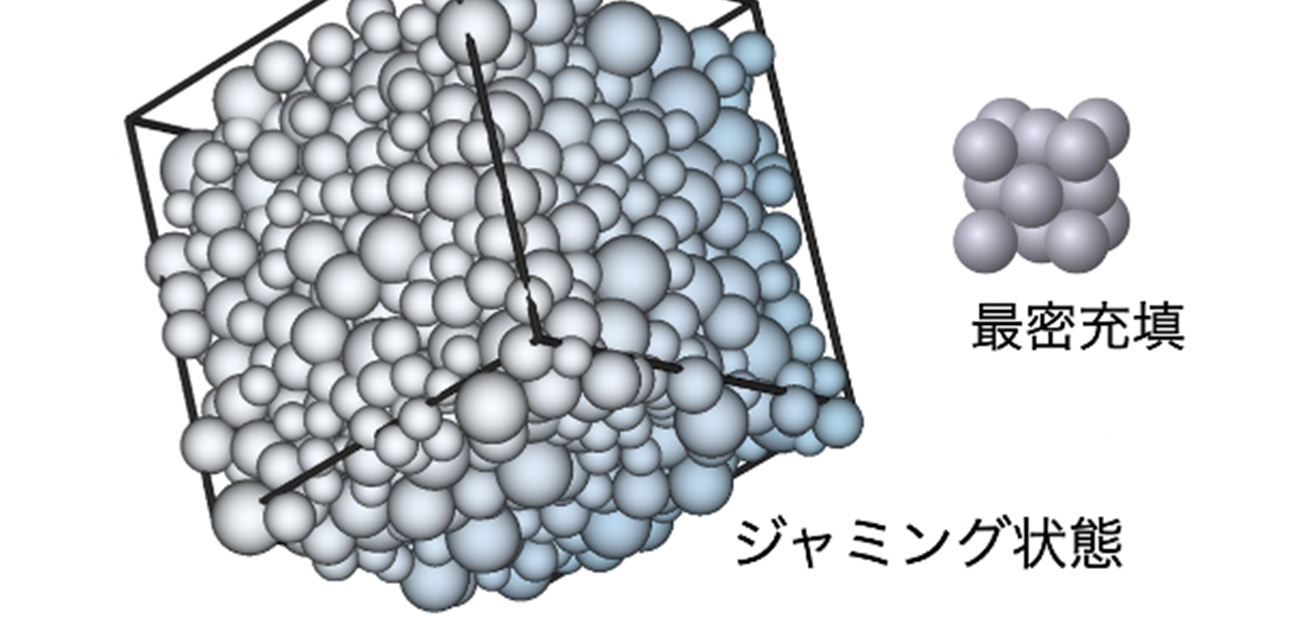
「きわどさ」に見つけた“普遍の法則”
ランダムにぎっしりと球を箱詰めするジャミングの物理をスーパーコンピューターで解明
研究成果のポイント
- 面心立方格子の結晶を限界まで圧縮してできる最密充填は唯一であるのに対し、「でたらめに」球を詰めてこれ以上詰められないジャミング状態は、圧縮の詳細によって多様な密度のものを作られることが知られていた。
- ジャミングは、マヨネーズや歯磨き粉など高密度のソフトマターの力学的性質を支配する重要な現象。
- 今回、スーパーコンピューターによる大規模計算によって、圧縮のみならず、シア(剪断)すなわち密度を変えずに容器を変形させてもジャミングできることがわかった。一方、こうした多様なジャミング状態が、すべてギリギリの安定性をもち、普遍的な臨界状態にあることが明らかになった。
- 多くの未解決問題が残るガラスの基礎物理の理解促進や、工業材料・食品に重要なコロイドなどの高密度ソフトマターの制御に役立つことが期待される。
概要
中国科学院理論物理研究所のYuliang Jin(ユリアン・ジン)准教授 (大阪大学サイバーメディアセンター招へい准教授)と大阪大学サイバーメディアセンターの吉野元准教授らの研究グループは、最もシンプルなガラス状態である剛体球ガラスに対して圧縮およびシア(剪断)をかける数値シミュレーションをスーパーコンピューターを用いて行いました。その結果、様々な密度と異方性をもつジャミング状態の生成に成功しました。ジャミング状態について詳しく調べると、これらが力学的にギリギリの安定状態であり、同一の臨界性を持つことが明らかになりました。本研究の成果により、身近にありながら結晶に比べて多くの未解決問題をもつガラスの基礎物理の理解が進展すると期待されます。
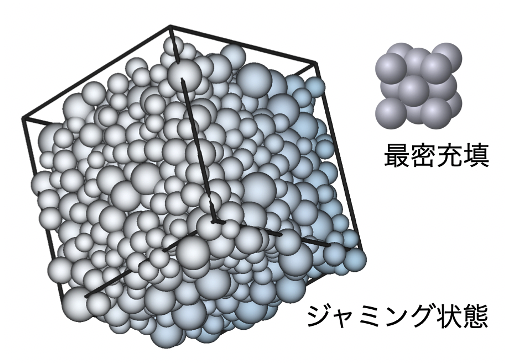
図1. ジャミング密度近傍にある高密度の剛体球ガラス
研究の背景
球を最も密に箱に詰める方法(最密充填)は、古くから議論されていました。17世紀にJ. ケプラーが3次元での最密充填は「面心立方格子」であると予想し、400年ほど後の1998年になってトーマス・C・ヘイルズがこれを証明しました。最密充填の密度は、体積分率で測って0.74048…です。
これに対し、「でたらめに」球を詰める実験をJ.ベナールとJ.メイソンらが1960年に行い (J. Bernal, J. Mason, Nature 188 (4754), 910 (1960))、密度0.64付近でジャミング、すなわち「これ以上詰められない」、の状態が得られることを見出しました。彼らはこれを「ランダム最密充填」と呼びました。しかし、その後の研究で、ランダムに詰めたジャミング状態は、圧縮を始める前の初期状態の作り方などによって様々な密度のものが得られることがわかってきていました。ジャミングはマヨネーズや歯磨き粉など高密度のソフトマターの力学的性質を支配する重要な現象です。
研究の内容
本研究グループでは、圧縮だけでなく、体積一定のまま箱を変形させるシア(剪断)によっても様々なジャミング状態が得られることを、スーパーコンピューターを用いた剛体球ガラスの大規模数値シミュレーションで見出しました。この現象は、粒子間に摩擦がある場合には知られていましたが、摩擦がなくても実現することが初めて示されました。さらに圧縮とシアを組み合わせて得られる様々な密度のジャミングがすべて共通した性質を持っていること、すなわち、これら全てが力学的にギリギリの安定性をもつ平均配位数6の状態にあること(図2左)、様々な物理量が共通した臨界現象を示すこと(図2右)を明らかにしました。
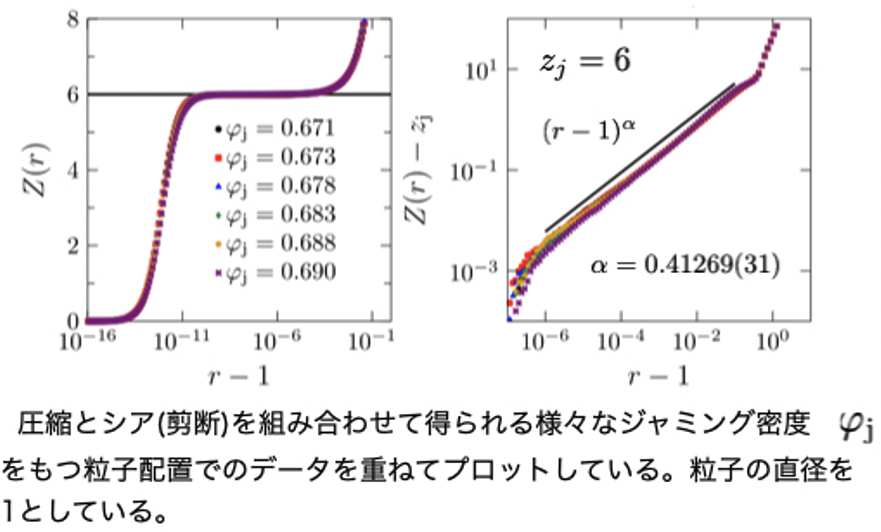
図2. (左図) 粒子の中心から距離rにある他の粒子の平均的な数 様々なジャミング密度を持つ配置で共通する普遍的な振る舞いになっている。左図から平均配位数は6であり、力学的にギリギリの安定状態にあることがわかる。また右図から、ほとんど接触しかけている粒子との距離は、普遍的な指数で特徴づけられるベキ分布に従っていることがわかる。これはある種の臨界状態にあることを示唆する。
本研究成果が社会に与える影響(本研究成果の意義)
本研究成果により、結晶とは異なり、乱れたまま固体となったガラスの基礎的理解が進むことが期待されます。また将来的には、身近な工業材料や食品において重要なコロイドなど、高密度のソフトマターの制御に役立つと期待されます。
特記事項
本研究成果は、2021年4月6日に米国科学誌PNAS(Proceedings of the National Academy of the United States of America)に掲載されました。
タイトル:“A jamming place of sphere packings”
著者名:Yuliang Jin and Hajime Yoshino
なお、本研究は、科研費基盤研究B「スピンから捉えるガラス・ジャミング転移の物理:ソフトマターから情報統計力学まで」の助成を受けて行われました。
参考URL
SDGs目標

用語説明
- 面心立方格子
図1の右上に示した構造。3次元での最密充填構造である。
- ジャミング
例えばパチンコ玉をざっと容器に流し込むと玉が、でたらめに、しかしぎっちりと詰まった状態になる。これが典型的なジャミング状態である。身の回りにも歯磨き粉など、高密度のコロイド粒子が集まってできた物質があり、ジャミングしかけているところでの振る舞いが実用上大切である。
- 平均配位数
粒子一つあたり、これを取り囲む他の粒子が平均的に幾つあるか、という数である。面心立方格子では12である。ジャミングでは6であるが、これはすべての粒子の動きを止めるのに必要なギリギリの数であり、一つでも欠けると系は動きだしてしまう。
