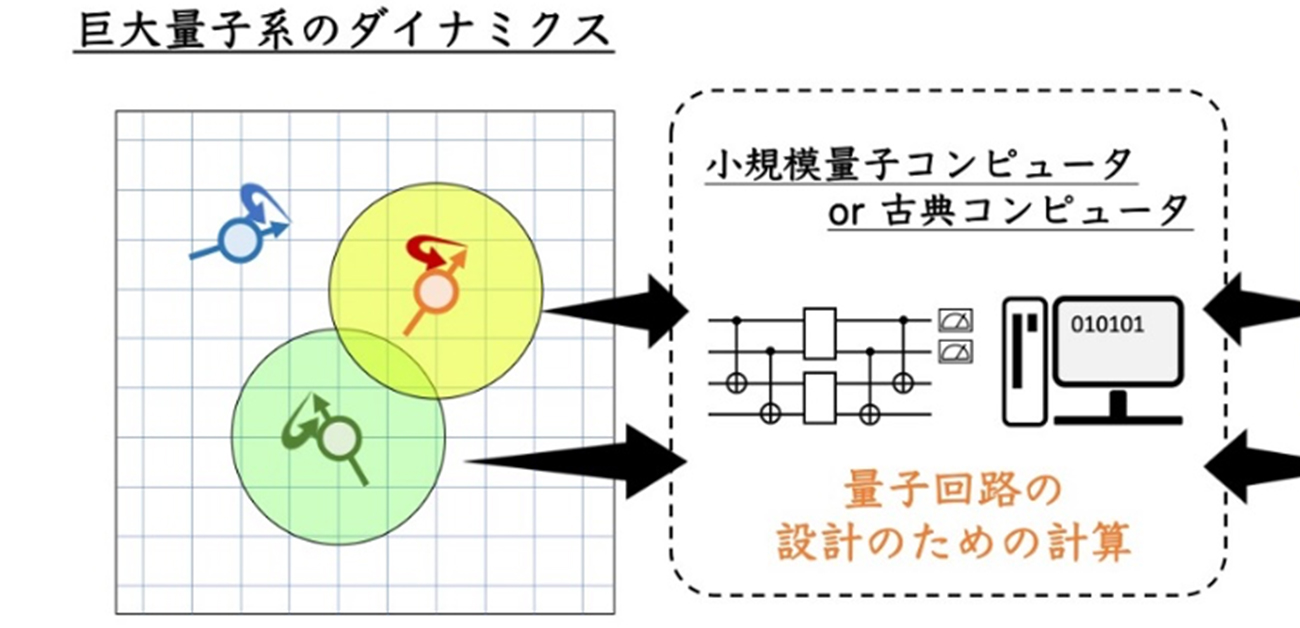
巨大量子系シミュレーション用の量子回路設計法を構築
物性・材料・化学計算への効率的・高精度な大規模量子計算を加速
概要
理化学研究所(理研)量子コンピュータ研究センター量子計算理論研究チームの水田郁基礎科学特別研究員、藤井啓祐チームリーダー(大阪大学大学院基礎工学研究科教授)、株式会社QunaSysの中川裕也リードサイエンティスト、大阪大学大学院基礎工学研究科の御手洗光祐助教らの共同研究グループは、「大規模な量子系のダイナミクス」を高精度に計算する量子回路の効率の良い設計法を構築しました。
本研究成果は、広範な量子系に対して効率的かつ高精度な大規模量子計算を可能にする手法として、物性・材料・化学分野への実用的問題への量子コンピュータの応用を加速するものと期待できます。
大規模な量子系のダイナミクスのシミュレーションは従来(古典)コンピュータでは実行困難であることから、量子コンピュータの最も重要なアプリケーションとして特に注目されています。しかし、このようなダイナミクスを高精度にシミュレートするには複雑な量子回路が必要であり、現在実現している規模の量子コンピュータでは実行できないという問題がありました。
「Lieb-Robinson限界」は情報が伝播する速度限界を与える理論であり、幅広い量子系で普遍的に成立します。今回、共同研究グループはLieb-Robinson限界を用いることで、小規模量子コンピュータや古典コンピュータでも大規模な量子系のダイナミクスをコンパクトかつ高精度に計算する量子回路を設計できることを証明し、その具体的なアルゴリズムの提案と数値検証を行いました。
本研究は、オンライン科学雑誌『PRX Quantum』(10月5日付:日本時間10月6日)に掲載されました。
図. 巨大量子系(大規模な量子系)のダイナミクスの量子回路を効率よく構成するアルゴリズムの概念図
研究の背景
量子コンピュータは、量子重ね合わせや量子もつれなどのミクロな世界に特有の量子力学的性質を利用することで、さまざまな問題を従来コンピュータ(古典コンピュータ)よりもはるかに高速で計算できると期待されています。中でも、「量子系のダイナミクス」をシミュレート(計算)する問題への量子コンピュータの応用は、物性物理・量子化学、そしてその先にある材料科学や化学など広範な分野への応用が期待される有望な使途と考えられています。
量子コンピュータ上での計算は、1量子ビットゲートや2量子ビットゲートなどの単純なゲートを組み合わせた量子回路を用いて行われますが、量子コンピュータのノイズや計算時間の観点から、計算に用いるゲートの個数は少ないことが望まれます。量子系のダイナミクスを計算する問題においても、できるだけ少ない数の基本ゲートで正確に量子系のダイナミクスを再現する量子回路をどのように設計するか、が特に重要な課題です。
量子系のダイナミクスを計算する量子回路の設計には、古くから時間を微小に分割・離散化する「鈴木-Trotter 分解」と呼ばれる手法が用いられてきました。この手法は単純ではあるものの、高精度な大規模量子計算を行うには実現困難な大量のゲートが必要です。そこで近年では、より大規模な量子系に応用され得る手法として、現在実現している規模の量子コンピュータ(NISQ)でも動作する変分量子アルゴリズムに基づいた量子回路の構築法が盛んに研究されてきました。
しかし、これまでの変分量子アルゴリズムに基づく手法では、目的の大規模な量子系のダイナミクスを少ないゲート数で計算する量子回路を設計するために、その目的のダイナミクス自体をあらかじめ量子コンピュータで実現しなければならない、というある種本末転倒な問題を抱えていました。
研究手法と成果
共同研究グループは、物理的に自然な仮定の下で情報の伝播する速度限界を与える理論である「Lieb-Robinson限界」によって、効率的かつ高精度に量子系のダイナミクスを計算する量子回路の設計手法の構築に成功しました。
まず、設計した量子回路がどのぐらい正確に量子系のダイナミクスを再現するかの誤差の指標を表す(変分量子アルゴリズムの)コスト関数の効率的な計算法を構築しました。このコスト関数は、目的の量子回路をコンパクトかつ高精度に設計するために量子コンピュータで計算される必要がある一方で、多くのゲートを使った大規模量子コンピュータを必要とするため、その直接的な計算は困難だと考えられています。そこで、コスト関数を効率よく計算するために、「Lieb-Robinson限界(図1(a))によって、量子系の時間変化の情報はその伝播する小さな範囲内を調べれば分かる(図1(b))」という事実に着目しました。この事実を量子系の時間変化の情報の一種と解釈できるコスト関数に応用することで、目的の大規模な量子系の量子回路を設計するためのコスト関数を、情報が伝播し得る範囲の小規模な量子系のコスト関数で計算できるという性質を明らかにしました。
図1. Lieb-Robinson限界
(a) 量子系の情報(スピンなど)が時間経過とともに徐々に広がっていく様子。物理的に自然な仮定の下では情報の広がる速度には限界があり、これを Lieb-Robinson限界と呼ぶ。
(b) Lieb-Robinson限界の見方を変えたもの。ある地点の量子系の時間変化の情報は量子系全体ではなく、その時刻までに情報が伝わった領域の範囲内の小規模な量子系を調べれば分かるといえる。
本研究で確立した手法では、このコスト関数の性質に基づいて、図2のように情報の伝播する範囲の量子系でコスト関数を計算することで、全体の量子系のための量子回路を設計します。情報の伝播する範囲は目的の大規模な量子系でも全体に比べて非常に小さく、そのコスト関数の計算には大規模量子コンピュータを必要としません。すなわち、本手法により、小規模量子コンピュータまたは古典コンピュータの計算結果のみによって、大規模な量子系のダイナミクスをコンパクトかつ高精度に計算する量子回路を設計することができます。
図2. 本研究で確立された手法の概要
最初に、図1(b)のLieb-Robinson限界で決まる大きさを決定する。その分の大きさのコスト関数を小規模量子コンピュータまたは古典コンピュータで計算する。そのコスト関数の最適化によって設計された量子回路によって、目的の巨大量子系(大規模な量子系)のダイナミクスを再現する量子回路が構成される。
本手法の具体的検証として、物性分野で最も単純な模型である1次元ハイゼンベルグ模型に対する数値実験を行いました。数十量子ビットの量子コンピュータにおける本手法の挙動を、古典コンピュータで再現しました。その結果、本手法では 鈴木-Trotter 分解という従来手法と比べて、同じゲート数で約100倍精度よく量子系のダイナミクスを計算できることが分かりました(図3(a))。さらに、最適化された量子回路を繰り返し用いることで、より長時間スケールのダイナミクスも効率よく計算できることを明らかにしました(図3(b))。
図3. 本手法の性能の検証結果
(a) 20~40量子ビットを持つ巨大な量子系に対して、20量子ビットの小規模量子系で最適化し、効率的な量子回路を設計した結果。グラフは、設計した量子回路のダイナミクスに対する誤差の大きさを2種類のコスト関数で評価したもので、同じ色の線は同じ種類を表す。コスト関数ごとに標準的な手法の鈴木-Trotter分解と比較すると、本手法は約100倍の精度(約100倍誤差が小さい)を達成している。
(b) 本手法で設計した量子回路を繰り返し利用し、長時間の量子系の時間変化を計算した結果。ゲート数が少ないにもかかわらず、長時間スケールでも正確な計算結果と合致している。
今後の期待
本研究で開発した手法は、量子回路を設計するための計算の過程がLieb-Robinson限界で決まる小規模の量子系で閉じています。それ故に、目的の大規模な量子系のダイナミクスをあらかじめ正確に再現する必要なく、小規模量子コンピュータまたは古典コンピュータを用いて効率よく計算する、コンパクトで高精度な量子回路を設計することができます。そのため、大規模な量子系のダイナミクスの計算という、古典コンピュータでは困難な量子コンピュータの最も重要なアプリケーションの実現を加速するものと期待できます。
本手法は、Lieb-Robinson限界という広範な量子系の持つ普遍的性質のみに依拠することから、大規模サイズ・長時間スケールのダイナミクスの効率的な量子計算に汎用的に役立ち、物性・材料・化学分野で関心の対象となるさまざまな量子物質に応用可能だと考えられます。
また、量子系のダイナミクスを計算する量子回路は単に量子系の時間発展を計算するだけでなく、エネルギー固有値・固有状態などの実応用の面で重要なさまざまな性質を計算できる量子位相推定アルゴリズムなどの中でも多用されています。今後、本研究成果がさまざまな目的に利用されることで、より広範な量子アルゴリズムの効率化に貢献すると期待できます。
特記事項
論文情報
<タイトル>Local variational quantum compilation of a large-scale Hamiltonian dynamics
<著者名>Kaoru Mizuta, Yuya O. Nakagawa, Kosuke Mitarai, and Keisuke Fujii
<雑誌>PRX Quantum
共同研究グループ
理化学研究所 量子コンピュータ研究センター 量子計算理論研究チーム
基礎科学特別研究員 水田 郁 (ミズタ・カオル)
チームリーダー 藤井 啓祐 (フジイ・ケイスケ)
(大阪大学大学院基礎工学研究科 教授)
株式会社QunaSys
リードサイエンティスト 中川 裕也 (ナカガワ・ユウヤ)
大阪大学大学院 基礎工学研究科 システム創成専攻
助教 御手洗 光祐 (ミタライ・コウスケ)
研究支援
本研究は、日本学術振興会(JSPS)卓越大学院プログラム「先端光・デバイス創成学」、科学研究費助成事業特別研究員奨励費「共鳴的周期駆動がもたらす非平衡特有の物性現象に関する研究(研究代表者:水田郁)」、同研究活動スタート支援「第一原理計算応用に向けた量子回路パラメータの効率的な初期化方法の構築(研究代表者:御手洗光祐)」、科学技術振興機構(JST)さきがけ「量子計算における低レイヤータスク分割技術の構築(研究代表者:御手洗光祐)」、同ERATO「中村巨視的量子機械プロジェクト(研究総括:中村泰信)」、同CREST 「冷却原子の高度制御に基づく革新的光格子量子シミュレーター開発(研究代表者:高橋義朗)」、同共創の場形成支援プログラム(COI-NEXT)「量子ソフトウェア研究拠点」、文部科学省光・量子飛躍フラッグシッププログラム(Q-LEAP)「知的量子設計による量子ソフトウェア研究開発と応用(研究代表者:藤井啓祐)Grant No. JPMXS0120319794」「量子コンピュータのための高速シミュレーション環境構築と量子ソフトウェア研究の展開(研究代表者:藤井啓祐)Grant No. JPMXS0118067394」による助成を受けて行われました。本研究の一部は、内閣府総合科学技術・イノベーション会議の戦略的イノベーション創造プログラム(SIP)「光・量子を活用したSociety 5.0 実現化技術(管理法人:量子科学技術研究開発機構(QST))」によって実施されました。
用語説明
- 量子系のダイナミクス
シュレディンガー方程式という量子力学における運動方程式によってもたらされる、物理系の時間変化。
- 量子コンピュータ
量子物理の原理に従って計算を行うコンピュータ。従来のコンピュータ(古典コンピュータ)にはない量子重ね合わせや量子もつれを利用することで、素因数分解などのさまざまな問題を高速で解けると期待されている。
- Lieb-Robinson限界
1972年にE. H. LiebとD. W. Robinsonらによって証明された性質で、相互作用が近くにしか及ばない一般の量子多体系では時間変化による情報の伝わる速さに限界があることを指す。近年ではさまざまな研究者によって、相互作用が長距離に及ぶ場合でもLieb-Robinson限界が存在し得ることが発見されている。
- 量子重ね合わせ、量子もつれ
量子重ね合わせは、ビットの「0」と「1」など複数の状態を同時に確率的に占有できることを指し、量子物理の世界に特有の効果として複素数の重みを持ち得ることが知られている。量子もつれは、エンタングルメントとも呼ばれ、量子重ね合わせとの組み合わせで生じる量子物理特有の相関である。
- 量子ビットゲート
古典コンピュータにおいてNOTゲートやANDゲートなどがビットを操作するように、量子コンピュータにおいて量子ビットを操作するための素子のこと。例として、パウリXゲートやCNOTゲートなどがある。
- 鈴木-Trotter 分解
量子系のダイナミクスを最も単純にゲートで再現する標準的な手法。量子回路の構造が簡素で現時点での数十量子ビットの量子コンピュータでも実装されている。しかし、精度よくダイナミクスを再現するには大量の量子ゲートが必要になるという欠点が知られている。
- NISQ
ノイズによって生じる計算の誤差を訂正することができない、数百量子ビット以上を有する中規模サイズの量子コンピュータの総称である。変分量子アルゴリズムなどの応用を通じて、数年~十数年程度の近い将来で実用化が期待されている。NISQ はNoisy Intermediate-Scale Quantum computersの略。
- 変分量子アルゴリズム
パラメータを持つ量子回路(変分量子回路)を設定し、量子コンピュータによるコスト関数の測定と、古典コンピュータによるコスト関数に基づいたパラメータの最適化を組み合わせて、問題を解くアルゴリズム。
- (変分量子アルゴリズムの)コスト関数
変分量子アルゴリズムにおいて、設定した変分量子回路がどれほど対象となる問題の解に到達できているかを指し示す関数。コスト関数が最大化あるいは最小化したときに変分量子回路が問題の解と一致するように設定される。
- ハイゼンベルグ模型
隣り合う電子間でスピンが同じ向き、あるいは逆向きにそろおうとする相互作用が等方的に働く模型。磁性やトポロジカル物性など物質の基本的性質の理解に重要な模型であると考えられている。
- エネルギー固有値・固有状態
ハミルトニアンという量子系のエネルギーを表す行列の固有値と固有状態。最も小さな固有値を持つ固有状態を基底状態、それ以外の固有状態を励起状態と呼ぶ。これらは、量子系の平衡状態やその付近のダイナミクスを決定する重要な量子系の情報である。
- 量子位相推定アルゴリズム
量子ゲートを行列で表したときの固有値と固有状態を高精度に計算するための量子アルゴリズム。
