大阪大学産業科学研究所の林克彦助教らの研究グループは、テンソル データを低ランクの二値潜在ベクトル空間 へと分解する手法を開発しました。

二値化 により、ベクトル空間の容量が単純には1/32に縮約され、検索の速度は約10倍に高速化されます。

これまでのテンソル分解（ここではCP分解 を対象）ではテンソルを低ランクの実数潜在ベクトル空間へと分解するのが一般的であり、二値潜在ベクトル空間では分解性能を著しく悪化させる危険性がありました。

今回、林助教らの研究グループは、潜在ベクトル空間の学習時に量子化関数 を導入することで分解性能を落とすことなく、二値化を実現しました。これにより、情報検索システムの軽量化・高速化が可能になります。

本研究成果は、国際会議「41st European Conference on Information Retrieval」に採録され、2019年4月15日（月）13時（中央ヨーロッパ夏時間）に発表を行いました。

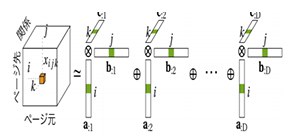
図1　二値化CPテンソル分解の概念図と空間の縮約・検索速度性能

テンソルデータを低ランクの実数潜在ベクトル空間へと分解（テンソル分解）することで、データに内在する潜在的な特徴量を抽出することができます。テンソル分解の応用先の1つとして文書検索があり、類似した文書の意味的な近さをベクトル空間の内積や距離で計量することができます。一方、ベクトル空間での検索はモデルの容量が大きく、検索効率も悪いことが知られており、この課題を解決する方法の1つとして、潜在ベクトル空間を二値化することが考えられます。しかし、二値化は元のデータを近似する際の誤差が増大するため、分解性能が著しく悪化する危険性がありました。

林助教らの研究グループでは、テンソル分解に対して、潜在ベクトル空間の学習時に量子化関数を導入することで、分解の性能を落とすことなく、潜在ベクトル空間を二値化することに成功しました。これによりベクトル空間の容量を単純には1/32に縮約でき、ベクトルの内積計算を高速化することができます。

本研究成果により、セマンティックWeb検索等の情報検索システムの軽量化・高速化につながることが期待されます。さらに、テンソル分解は画像圧縮等への応用も知られており、提案法はさらなる応用の可能性を秘めています。

本研究成果は、2019年4月15日（月）13時（中央ヨーロッパ夏時間）〔4月15日（月）20時（日本時間）〕に情報検索に関連する国際会議「41st EuropeanConference on Information Retrieval」で発表を行いました。

タイトル：“Binarized Knowledge Graph Embeddings”
著者名：Koki Kishimoto, Katsuhiko Hayashi, Genki Akai, Masashi Shimbo and Kazunori Komatani

なお、本研究は、科学研究費補助金・基盤研究（C）の一環として行われました。