Faster information retrieval system achieved by binarized Knowledge Graph Embeddings
A group of researchers led by Assistant Professor Katsuhiko Hayashi from the Institute of Scientific and Industrial Research of Osaka University developed a binarized CANDECOMP/PARAFAC (CP) tensor decomposition algorithm for machines to learn compact knowledge graph embeddings (KGE), improving memory footprints and reducing score computation time without a decrease in task performance.
A knowledge graph (KG) is a knowledge base which describes and stores facts as triples. Each triplet represents a fact that relation holds between subject entity and object entity. Since most KGs are far from complete, it is necessary to fill in the missing triples in carrying out various inference over KGs. Knowledge graph completion (KGC) aims to perform this task automatically.
KGE has been actively pursued as a promising approach to KGC. In KGE, entities and relations are embedded in vector space and operations in this space are used for defining a confidence score function that approximates the truth value of a given triple.
The vector space model, an algebraic model for representing text documents, is used for information retrieval. In vector space, words are represented as vectors and all vectors have a certain direction and it is possible to explicitly define their relationship with each other. The inner product of a vector that represents the direction of two vectors is used for comparing documents by measuring the distance between these features.
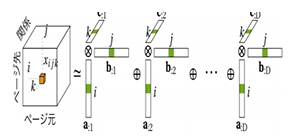
The tensor is a more generalized form of scalar and vector: a rank 0 tensor is called scalar and rank 1 tensor is called vector. Latent features in data can be extracted through low-rank tensor decomposition, which has been successfully applied to information retrieval. However, even with a simple model like CP tensor decomposition, KGC on existing KGs is impractical because a large amount of memory is required to store parameters represented as 32-bit or 64-bit floating point numbers.
To reduce memory footprints and shorten score computation time, the group proposed a new CP decomposition algorithm, a method for binarizing the parameters of the CP tensor decomposition by introducing a quantization function to the optimization problem.
After training, the binarized embeddings can be used in place of the original vectors, drastically reduces the memory footprint of the resulting model, making search speeds ten times faster. Traditional tensor decomposition methods, such as CP decomposition, aim to factorize an input tensor into a number of low-rank factors; however, binarization of low-rank approximation of a given tensor will increase errors, degrading task performance.
In this study, by introducing the quantization function to tensor decomposition in machine learning of latent vector space, the group binarized a latent vector space with acceptable minor performance degradation. Binary vector representations compress vector space to 1/32, contributing to efficiently computing the inner product by using bitwise operations. The results of this study will minitualize and speed up semantic web search systems. Because tensor decomposition can also be used for graphical data compression, the method in this study has a wide range of potential applications.
Figure 1
The article, “Binarized Knowledge Graph Embeddings” was presented at the 41st European Conference on Information Retrieval. To learn more about this research, please view the full research report entitled “Binarized Knowledge Graph Embeddings” at this page .
Related links
