Discovery of the complexity of the quark, a fundamental constituent of matter
Formulation of a chaos index in movement of
The Lyapunov exponent is a measurement tool for chaotic systems. A larger Lyapunov exponent is usually taken as an indication that the system is more chaotic, so the exponent is a useful measure for knowing difficulty in quantifying predictability. However, Lyapunov exponents are calculated from the positions and velocities of particles, so it was difficult to calculate Lyapunov exponents for particle physics that deals with the smallest physical systems, in which the positions and velocities of particles could not be identified.
In particle physics in which the principle of quantum mechanics is applied, it’s not possible to measure both positions and velocities at the same time. Quarks, in particular, are highly affected by the quantum effect , so they behave strangely. No free quarks can exist on their own and quarks clump together to form groups, so, for individual quarks, situations in which Lyapunov exponents are calculated were not known.
Professor HASHIMOTO Koji at the Graduate School of Science, together with Assistant Professor MURATA Keiju at the Department of Physics, Hiyoshi Campus, Keio University and Assistant Professor Kentaroh Yoshida at the Graduate School of Science, Kyoto University, succeeded in calculating a chaos index for dynamics of generic quantum field theories, a world first.
The complexity of a chaotic system is described by chaos theory. For elementary particles that constitute the universe, chaos theory was applied only to the elementary particle boson, a force carrier which mediates the weak force. Of 17 elementary particles, it was difficult to apply chaos theory to fermions such as quarks.
This group solved this challenge by using a new method, holographic principle, which has developed in particle physics in recent years. This group succeeded in calculating Lyapunov exponents of elementary particles, demonstrating that chaos existed in the motion of quarks.
The extension of applications of chaos theory to quarks, which is difficult to analyze in a quantum-mechanical manner, is a step toward the clarification of the complexity of the standard theory of elementary particles. It is hoped that this study will deepen the understanding of why nature chooses the standard theory of elementary particles.
Abstract
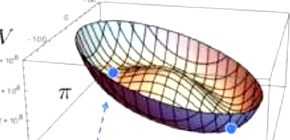
Assigning a chaos index for dynamics of generic quantum field theories is a challenging problem because the notion of a Lyapunov exponent, which is useful for singling out chaotic behavior, works only in classical systems. We address the issue by using the AdS / CFT correspondence, as the large N c limit provides a classicalization (other than the standard ℏ → 0 ) while keeping nontrivial quantum condensation. We demonstrate the chaos in the dynamics of quantum gauge theories: The time evolution of homogeneous quark condensates ⟨ ¯ q q ⟩ and ⟨ ¯ q γ 5 q ⟩ in an N = 2 supersymmetric QCD with the S U ( N c ) gauge group at large N c and at a large ’t Hooft coupling λ ≡ N c g 2 YM exhibits a positive Lyapunov exponent. The chaos dominates the phase space for energy density E ≳ ( 6 × 1 0 2 ) × m 4 q ( N c / λ 2 ) , where m q is the quark mass. We evaluate the largest Lyapunov exponent as a function of ( N c , λ , E ) and find that the N = 2 supersymmetric QCD is more chaotic for smaller N c .

Figure 1

Figure 2
To learn more about this research, please view the full research report entitled “ Chaos in Chiral Condensates in Gauge Theories ” at this page of the Physical Review Letters website.
Related link
- Particle Physics Theory Group, Graduate School of Science, Osaka University (link in Japanese)

