大阪大学大学院基礎工学研究科 廣畑佑真さん（博士後期課程）、杉山和靖教授（理化学研究所光量子工学研究センター 客員研究員兼任）、関西大学システム理工学部 関眞佐子教授、板野智昭教授、佐井一総さん（修士課程（当時））、丹下祐希さん（修士課程（当時））、 西山朋宏さん（修士課程）、岡山大学学術研究院環境生命自然科学学域 鈴木大介教授、湊遥香講師（特任）らの研究グループは、マイクロ流路内における粒子の集束パターンが粒子の慣性と変形性によって劇的に変化することを明らかにしました。硬い粒子が流路の壁近くに集まるのに対し、やわらかいヒドロゲル粒子は流路断面の中心や対角線上に集まることを実証しました。

さらに、スーパーコンピュータ「富岳」を活用したコンピューターシミュレーションや、新たな理論モデルに基づく解析により、レイノルズ数とキャピラリー数をパラメーターとする相図を作成し、集束パターンが劇的に変化する「相転移」の条件や、その背景にある物理の仕組みを明らかにしました。この成果は、液体の中の細胞や粒子の変形性を利用した次世代のマイクロ流体デバイス開発につながり、高効率な細胞選別技術として、がんの早期発見など医工学分野への応用が期待されます。

本研究成果は、流体力学に関する専門学術誌である「Journal of Fluid Mechanics」に、2025年９月１８日付で公開されました。

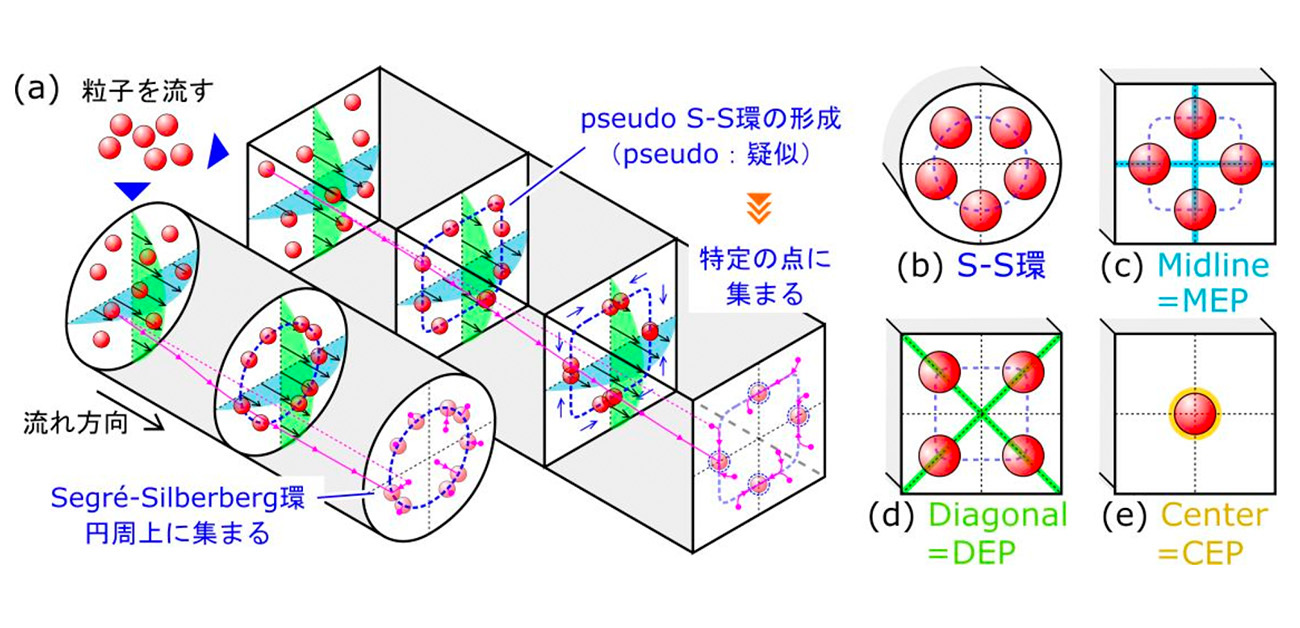
近年、小さな水の通り道「マイクロ流路」を使って、液体の中の細胞や粒子を望みどおりに動かす技術が注目されています。この技術は、病気の細胞を効率よく選び分けるなど、がんの早期発見や治療に役立つと期待されています。特に、体から直接細胞を採取する従来の組織生検とは異なり、血液や体液からがん細胞等を解析する、体への負担が小さく、繰り返し検査できるリキッドバイオプシーと呼ばれる新しい技術への期待が高まっています。マイクロ流路の中を流れる粒子は、流れの勢い（慣性）によって、流路断面内の決まった場所に集まる性質があります(図1(a))。流路断面が円形の場合、硬い球形粒子はSegre-Silberberg環と呼ばれる円周上に集まることが知られています（図1(b)）。一方で流路断面が正方形の場合、粒子が壁に近い4つの点に集まるMEPパターン(図1(c))を示すことが、関教授のグループの管断面を正面から観察する手法によって確認することができます。細胞を効率よく選別するには、細胞を一点にしっかり集めることが重要ですので、角のある四角い流路が優れています。

実は、がん細胞や病気の細胞は、健康な細胞に比べて変形のしやすさ（変形性）が違うことがわかっています。この性質の違いを利用することで、より正確に細胞を選び分けられることに着目しました。最近のコンピューターシミュレーションによる研究では、正方形断面を持つ流路にやわらかい粒子を流したときに、対角線上にある4つの点に集束するDEPパターン（図1(d)）や、流路の中心に集束するCEPパターン（図1(e)）を示すことが予測されました。しかし、やわらかい粒子を使った実験は難しく、やわらかさが粒子の集まり方（集束パターン）にどう影響するのか、詳しいことはわかっていませんでした。

図1. (a)円管と正方形管における粒子集束の様子と(b)-(e)粒子が集まる主なパターン。(b)Segre-Silberberg環 (c)MEP (d)DEP (e)CEP ※EP=Equilibrium Position（集束位置）

研究グループは、マイクロ粒子のやわらかさ、寸法、形状を均一にできるヒドロゲル粒子を用いることにより、変形性を厳密に研究できる実験と、スーパーコンピュータ「富岳」などを使った計算を組み合わせることで、「慣性」と「変形性」が粒子の集まり方に決定的な影響を与えることを明らかにしました。

【成果１ 細胞と同じくらいの大きさの、やわらかい粒子を作ることに成功！】
　細胞は数マイクロメートル程度のものが多いですが、ヒドロゲル粒子でこの大きさの粒子を作製するのは一般的に困難とされてきました。従来の粒子はこれよりずっと小さく、１マイクロメートル以下の大きさでした。鈴木教授のグループでは、これまで、架橋構造を変化させることで、粒子の硬さをコントロールし、やわらかさ、寸法、形状を均一にする技術を確立しました。この技術を使って、細胞と同じくらいの大きさの、やわらかい「ヒドロゲル粒子」の生成に成功しました。

【成果2 やわらかさによって集まる場所が変わることを実験で証明！】
やわらかい粒子を四角い流路に流して、その動きを観察しました。その結果、硬い粒子とは異なり、流路の真ん中や対角線上の4つの点に集まることを実験で示しました。これにより、粒子のやわらかさによって集まり方が大きく変わるというコンピューターシミュレーションによる予測の正しさが証明されました。

【成果3 粒子の集まり方がガラッと変わる条件を発見！】
四角い流路を流れるやわらかい粒子の動きをコンピューターシミュレーションによって予測しました（図2(a)）。研究グループはスーパーコンピュータ「富岳」の計算能力を利活用して、100以上の異なる条件を調べることで、慣性の程度を表す「レイノルズ数」と変形性の程度を表す「キャピラリー数」という2つの要因から、粒子の集まり方がどのように変化するのかを表すマップ （図2(b)） を作成しました。このマップから、やわらかさが増すにつれて、粒子の集まり方がMEPから8つの集束点（MEPとDEPの混合）、DEP、そしてCEPへと劇的に変化する「相転移」が起こる条件を突き止めました。

【成果4 相転移の謎を理論的に解明！】
さらに、なぜこのような「集束パターンの相転移」が起こるのかを、新しい理論モデルによって数学的に説明しました。この理論により「レイノルズ数」と「キャピラリー数」の比を表す「ラプラス数」Laが「集束パターンの相転移」のカギを握っていることを明らかにしました。「ラプラス数」Laが特定の値をこえると、粒子は流路の中心に安定して留まれなくなり、集まり方が急変するのです。

図2. (a)コンピューターシミュレーションによる計算例 (b)粒子の集まり方を示したマップ

この研究は、粒子の「変形性」という新しいパラメーターを取り入れた次世代のマイクロ流体技術につながります。これまで経験に頼りがちだった流路の設計に、科学的な根拠を与えます。特に、新しい理論モデルは、非線形の問題を「慣性」と「変形性」の線形部分問題に分けて解くことから、設計を格段に効率化することも期待されます。本研究成果の活用によって、特定の細胞の選び分けが容易になれば、以下の医工学分野への応用が期待されます：

● がんの早期診断:正常な細胞に比べ，変形性が異なるがん細胞を素早く見つけ出すことで，早期発見の精度が上がります．
● 治療効果の確認: 治療によって変わった細胞のやわらかさを調べることで，治療がうまくいっているかを確認できます．

私たちは今後も研究を進め、この技術が医療やバイオテクノロジー分野で実際に役立つように取り組んでいきます。

本研究成果は、2025年９月１８日流体力学に関する専門学術誌である「Journal of Fluid Mechanics」（オンライン）に掲載されました。

タイトル：“Experimental and numerical study on the inertial migration of hydrogel particles suspended in square channel flows”
著者名：Hirohata, Y., Sai, K., Tange, Y., Nishiyama, T., Minato, H., Suzuki, D., Itano, T., Sugiyama, K. and Sugihara-Seki, M.
ＤＯＩ：https://doi.org/10.1017/jfm.2025.10574

なお、本研究の一部は、日本学術振興会科学研究費補助金（JP20H02072、 HP24K00809)、 科学技術振興機構 次世代研究者挑戦的研究プログラム(JPMJSP2138)の助成を受けて行われました。コンピューターシミュレーションの一部は、理化学研究所計算科学研究センター「富岳」（HPCI System Research Project hp220106）、 大阪大学 D3センター「SQUID」、九州大学情報基盤研究開発センター「玄界」を用いて実行しました。

杉山和靖 研究者総覧
https://rd.iai.osaka-u.ac.jp/ja/4f3be6b665b51b35.html