トポロジー✕機械学習で拓く物性シミュレーション

カタチからエネルギーをズバリと当てる新技術

2023-8-22●自然科学系

産業科学研究所教授南谷英美

複雑なアモルファス構造の持つエネルギーを、トポロジカルデータ解析とシンプルな機械学習モデルの組み合わせで高精度に予測できることを発見した
アモルファス構造を特徴づける原子の繋がり方の情報を抽出することが従来方法では困難であったが、トポロジーを応用することで可能になった
アモルファスを始めとする不規則系に対する高効率なシミュレーション手法へのさらなる展開が期待される

概要

大阪大学産業科学研究所の南谷英美教授、岡山大学AI・数理データサイエンスセンターの大林一平教授、東京大学大学院工学系研究科の清水康司助教・渡邉聡教授からなる研究グループは、トポロジーの情報と機械学習を組み合わせることで複雑なアモルファス構造のエネルギーを予測する新規手法を開発しました。

アモルファスは太陽電池やコーティング材料など幅広く応用されている材料です。その複雑な構造と物理的性質や機能の相関を解明するためには、新たなシミュレーション手法の開発が不可欠です。現在、最も有力な手法は、高精度な量子化学計算を再現する代用モデルを機械学習によって作成する機械学習ポテンシャルと呼ばれるものです。しかし、アモルファス構造の特徴をどのように機械学習モデルの入力データに反映するかという点が課題でした。

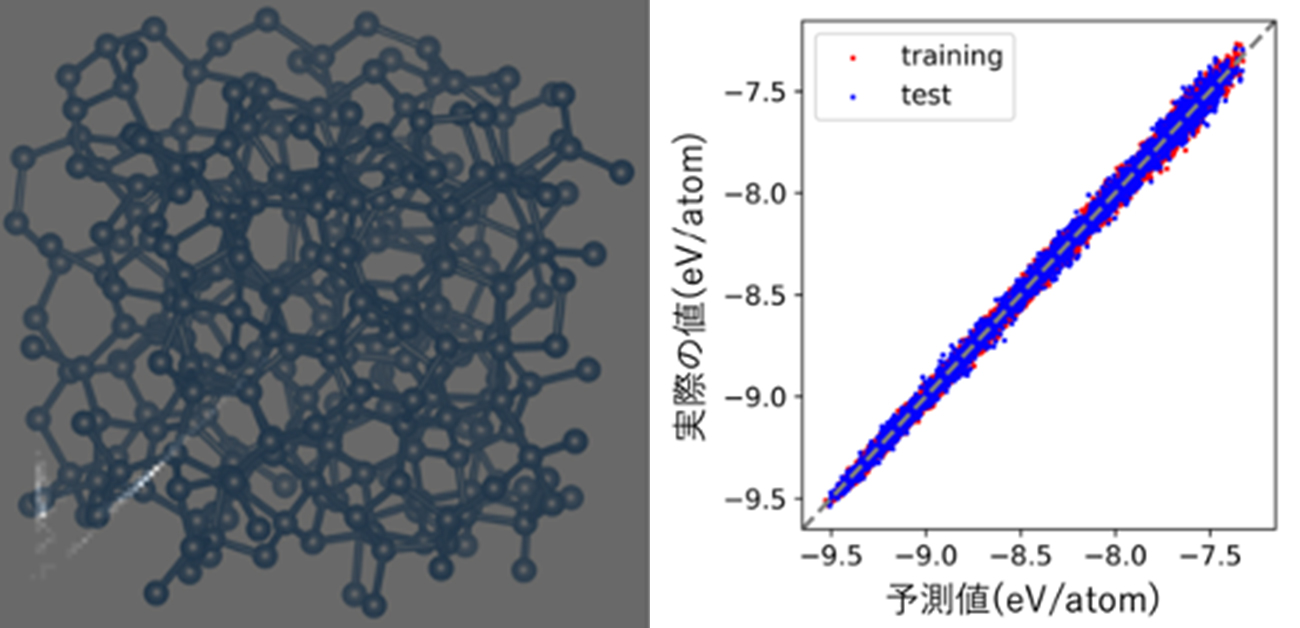
今回、南谷教授らの研究グループは、トポロジーという数学理論に基づくトポロジカルデータ解析を応用することにより、アモルファス構造内の原子の繋がり方の情報をより直接的に機械学習モデルに入力し、シンプルなモデルでもエネルギーの予測が可能であることを発見しました（図１）。これにより、複雑な構造を持った物質に対する高効率なシミュレーション技術の発展が期待されます。

本研究成果は、米国科学誌「The Journal of Chemical Physics」に、８月２２日（火）（現地時間）に公開されました。

図1. トポロジーの情報と機械学習の組み合わせによるアモルファス構造でのエネルギー予測

研究の背景

アモルファスに代表される乱れた複雑な構造と物質の性質がどのように関係しているかを理解することは、物質科学における難問の一つです。そのためには、高精度なシミュレーション手法が必要とされていますが、密度汎関数理論などに代表される量子化学計算は非常に計算コストが高く、アモルファスの物性を調べるために必要な沢山のサンプルに対する計算を迅速に行うことは困難です。これを解決する方法として、量子化学計算の結果を再現するような代用モデルを機械学習によって構築する、機械学習ポテンシャルが注目されています。アモルファスに応用した際の性能を引き上げるためには、アモルファス構造の特徴を反映したデータを機械学習モデルのインプットとして用いることが重要です。そのためには複数の原子の繋がり方を効率的に記述することが必要ですが、これまで用いられてきた原子間距離や角度の分布に基づく記述方法では困難でした。

研究の内容

本研究グループでは、トポロジカルデータ解析手法の一つ、パーシステントホモロジーを応用することで、原子の繋がり方の情報を直接的に機械学習モデルのインプットとし、シンプルなモデルでアモルファスカーボンのエネルギーを予測できることを示しました。

本研究ではまず、密度汎関数理論を用いて、様々な密度での液体状態とアモルファス状態の炭素の構造とエネルギーの高精度なデータを作成しました。そして、得られた構造の特徴を、パーシステントホモロジーを用いて解析しました。パーシステントホモロジーはパーシステント図と呼ばれる二次元平面上の点の分布として可視化されます（図２）。この図を多数の小さな正方形に分割し、各領域あたりに点がいくつ存在するかというヒストグラムの形式に変換し、その情報とエネルギーの計算結果を学習データとして機械学習を実行しました。その結果、最もシンプルなモデルの一つ、リッジ回帰モデルでも、エネルギーの予測ができることが明らかになりました。また、ヒストグラムを画像データのようにみなして、畳み込みニューラルネットワークを用いることで、予測性能が向上することも判明しました。

図2. 液体・アモルファス構造のカーボンに対するパーシステントホモロジーの計算結果（パーシステント図）と、それを用いたエネルギーの予測結果

なお、従来の原子間距離や角度の分布に基づく記述方法であっても、グラフニューラルネットワークなどの高度なアーキテクチャを用いると原子の繋がり方の情報を抽出できることが知られています。そこで、研究グループは、グラフニューラルネットワークを利用した場合とパーシステントホモロジーを用いた場合について、構造情報の捉えられ方を比較しました。その結果、パーシステントホモロジーを用いると、シンプルなモデルであってもグラフニューラルネットワークの場合と同様の情報を抽出できていることもわかりました。

本研究成果が社会に与える影響(本研究成果の意義)

本研究成果により、複雑な構造を持った物質に対する高効率なシミュレーション技術の発展が期待されます。また、今回の研究ではパーシステントホモロジーを用いることで、複雑な機械学習モデルを用いずとも構造からエネルギーを予測できました。その結果、「原子が作るどのような形が高い（低い）エネルギーに対応しているか」を解析することも可能になりました。このように、人が理解しやすい機械学習モデルを構築できる点は、望ましい性質を持ったアモルファスや不規則系の設計にも有用であると考えられます。

図3. 原子座標をデータとした場合に、パーシステントホモロジーの計算過程で繋がり方をどのように定義するかと、得られるパーシステント図の模式図。原子を中心とした球の半径を大きくしていって、球が接すると原子と原子の間に辺を置く。球の半径を大きくしていった際に、辺が増えていき閉じた環を作った半径 (birth time) を記録する。さらに球の半径を大きくして環が球ですべて被覆された半径 (death time) も記録する。その二つの半径の情報を散布図にしたものがパーシステント図である。

特記事項

本研究成果は、2023年8月22日（火）（現地時間）に米国科学誌「The Journal of Chemical Physics」（オンライン）に掲載されました。

タイトル：“Persistent homology-based descriptor for machine-learning potential of amorphous structures”
著者名：Emi Minamitani, Ippei Obayashi, Koji Shimizu, Satoshi Watanabe
ＤＯＩ：https://doi.org/10.1063/5.0159349

なお、本研究は、以下の研究費の助成を受けて実施されました。
・科学技術振興機構（JST）戦略的創造研究推進事業さきがけ
JPMJPR2198
（力学機能のナノエンジニアリング　領域）
JPMJPR1923
（数学と情報科学で解き明かす多様な対象の数理構造と活用　領域）

・科学研究費補助金
23H04470、23H04100、22H05106 、21H01816、21H05552、20H05884 、19H02544、19H00834

また、本研究のコンピューターシミュレーションには自然科学研究機構岡崎共通研究施設・計算科学研究センターのスーパーコンピューターを用いました。

参考URL

南谷英美教授研究者総覧
https://rd.iai.osaka-u.ac.jp/ja/9ee30fca5c7f9ac5.html

SDGsの目標

用語説明

トポロジー: 形状の繋がり具合を数学的に取り扱うことができる概念。原子・分子の構造に応用する場合には、原子の繋がり方に着目することに対応する。
アモルファス: 結晶のように原子が規則正しく並んだ状態ではなく、不規則に配列した固体。身の回りの代表例では窓ガラスや黒曜石が挙げられる。
機械学習ポテンシャル: 原子の持つエネルギーを予測するモデルとして機械学習モデルを利用するシミュレーション手法。高精度な量子化学計算の結果を学習データとしてモデルを訓練することで、量子化学計算の結果を再現するが計算速度は圧倒的に早い代用モデルを作ることができる。
トポロジカルデータ解析: トポロジーの考え方を応用したデータ解析手法の総称。データの繋がり方によって決まる環や空隙といった「穴」に対応する構造を、データの持つトポロジーと考えて定量化し、クラスタリングや回帰などのデータ解析に応用することができる。
密度汎関数理論: KohnとShamによって提案された電子密度から電子系のエネルギーなどの物理量を計算できる理論。この密度汎関数理論に基づいた第一原理計算手法は、原子番号と原子位置だけをパラメータとして現実物質の物性予測を可能とする、計算物質科学の強力な手法である。
パーシステントホモロジー: トポロジカルデータ解析の代表的な手法の一つ。データとデータの繋がり方や、その結果生じるデータの中の「穴」に対応する構造を、データ点を中心にした球の半径を増やしていったときの被覆のされ方で定義する点に特徴がある（図３）。どのスケールで「穴」が発生または消滅するかを数学のホモロジーと呼ばれる概念を用いて定式化する。この方法により、様々なスケールでの、データが持つトポロジーの情報を得ることができる。
リッジ回帰: 線形回帰に基づく手法の一つ。線形回帰では入力データ(x_1,…,x_n)から出力yを予測するモデルがy=w_0+w_1 x_1+⋯〖+w〗_n x_nであり、w_0,w_1,…,w_nを学習データに基づいて最小二乗法で最適化する。線形回帰を行う際、入力データの次元が大きいと過学習をしてしまうことがある。リッジ回帰では最適化に使う損失関数に正則化項を入れて過学習を抑制している。
畳み込みニューラルネットワーク: 生物の視覚情報処理を参考にしたアルゴリズムを用いる機械学習モデル。特に画像認識タスクにおいて強い性能を発揮する。畳み込み層と呼ばれる特定の形状を抽出するようなフィルターの機能を持った層を繰り返したような構造をしており、それぞれの畳み込み層が異なる形状やパターンを抽出する。
グラフニューラルネットワーク: 頂点が辺で結ばれたグラフの構造を持つデータに応用できる機械学習モデル。例えば、ソーシャルネットワークでは人が頂点、交友関係が辺となり、分子の場合では原子が頂点、原子間の結合が辺となる。グラフニューラルネットワークによる機械学習モデルを使うことで、「ある人とある人の間には交友関係があるか？」や、「ある分子には毒性があるか？」などの様々な予測を行うことが可能である。「グラフで表現される原子構造がどの程度のエネルギーを持つか？」を予想するタスクに応用することで、機械学習ポテンシャルに応用することができる。

キーワード

アモルファス機械学習ポテンシャルトポロジー SDGs

この研究についてひとこと

南谷英美