
ギネスビールの泡が織りなす模様を数式で。
泡と粒子の不思議な現象の解明
研究成果のポイント
- 泡が織りなす模様の発生条件を数式で記述
- コップに注いだ飲料の流れを実験や数値計算をせずに予測可能
- 泡や粒子が関連する流れの理解促進や流れの制御に期待
概要
大阪大学大学院基礎工学研究科の渡村友昭助教、杉山和靖教授、キリンホールディングス株式会社の四元祐子氏、鈴木深保子氏、若林英行氏らの研究グループは、コップに注いだギネスビールの泡が作り出す模様の発生条件を世界で初めて数式で表現しました。ギネスビールという黒ビールは窒素ガスが加圧封入されており、コップに注ぐとコーラや炭酸水に含まれる炭酸ガスの泡の1/10程度の微細な泡が発生し、また泡がコップの上から下へと移動する美しい模様(図1)が現れることが知られています。
これまで渡村助教らの研究グループは、ギネスビールの泡が織りなす模様は、雨水が傾斜面を下降する際に現れる模様【転波(てんぱ)】と同様であることを明らかにしてきました[1]。しかし、泡の模様は炭酸水やコーラでは見ることが出来ず、同じ泡でも模様の発生を決める要因は解明されていませんでした。今回、渡村助教らの研究グループは、スーパーコンピューターを使ったコンピューターシミュレーションと数理モデルを駆使し、泡と液体の運動を再現しました。その結果、泡が「密」に存在し集団的に振る舞う条件下において、気泡の模様が発生しえることを解明しました。さらに、コーラや炭酸水をドラム缶のように大きな容器に注げば模様が発生する可能性があることを示しました。この模様の発生条件を理解することで、食品・飲料の醸造や排水処理に用いる発酵槽の内部流動を予測することができるため、発酵食品の品質管理や水処理の高効率化に繋がることが期待されます。
本研究成果は、米国科学誌「Physical Review E」に、6月8日(火)午前0時(日本時間)に公開されました。

図1. ギネスビールの泡が織りなす模様 コップの内壁が傾斜している部分において、泡の粗密分布が自発的に形成されます。この模様は泡がコップの上から下へと移動する際に現れます。
研究の背景・内容
ギネスビールという黒ビールに含まれる泡は窒素ガスによって作られているため、炭酸水やコーラなどの炭酸飲料と比べて寸法が1/10ほど(直径50μm程度)にしか成長せず、ゆっくりと浮上します。無数の泡が飲料中に長く留まるため、クリーミーな味わいを楽しめると同時に、泡の集団が織りなす模様を鑑賞することもできます(図1および図2)。この美しい模様はビール愛好家以外にも、科学者達の心を惹きつけ、渡村助教らの研究グループは模様が発生する仕組みを既に明らかにしています(https://resou.osaka-u.ac.jp/ja/research/2019/20190411_1)。しかし、泡の模様はギネスビールを代表とした窒素封入飲料でしか見られず、コーラや炭酸水では見られません。今まで、泡の模様発生を説明することや予測することが出来ず、不思議な現象として扱われてきました。
飲料に含まれる泡の量や大きさを制御することは、一般的には不可能です。飲料を実験対象として扱う以上、限られた条件でしか実験を行えないため、模様の有無や気泡の運動について一般的な法則を見出すことは不可能でした。また、近年の目覚ましいスーパーコンピューターの発達をもってしても、小さな泡が膨大な数で存在する流れを三次元空間で完全に再現するコンピューターシミュレーションは、現代の計算科学でも超難問であると言えます。そこで、二次元で比較的難易度が高くないコンピューターシミュレーションと数理モデルを併用して、気泡が模様を作る条件の一般性を調べたのがこの研究です。
今回、渡村助教らの研究グループは、まず二次元のコンピューターシミュレーションを用いてギネスビールに現れる泡の模様を再現することを試みました(図3aおよび図3b)。コンピューターシミュレーションにより泡の模様を再現することに成功し、泡の量や大きさ、容器の大きさや壁面の角度を自由に設定したシミュレーションを約400条件も行いました。また、泡と液体の運動方程式を用いて数理モデルを作り、流れのスケーリング則を見出しました。模様の出現は「安定か不安定を表す指標(フルード数)」と「泡が密か疎かを表す指標(濃度界面の解像度[2、3])」という二つの要因によって決定することを示しました。この数理モデルにより、コップの形に応じた模様の有無(図3c)を説明することが可能となりました。また、コーラや炭酸水が一般的なコップでは模様を形成しない理由は、隣接する泡同士の距離が離れており「密」状態が回避されているため、であることが分かりました。さらに、この数理モデルを解釈すると、コーラや炭酸水をドラム缶の様に非常に大きなコップに注げば、相対的に密な状況を作り出せるため模様が現れる可能性があることが示唆されました。

図2. 様々な飲料の気泡が織りなす模様 気泡の模様を観察しやすいように左図のような台形のコップを作り、様々な飲料に含まれる気泡の運動を観察しました。右図は左から順にギネスビール、ハイネケンビール、シャンパン、コーラ、炭酸水。ギネスビール以外の飲料に含まれる気泡は模様を作りません。(今回の論文の補足情報として、以下のリンク先で実際の動画を入手いただけます。https://journals.aps.org/pre/supplemental/10.1103/PhysRevE.103.063103)
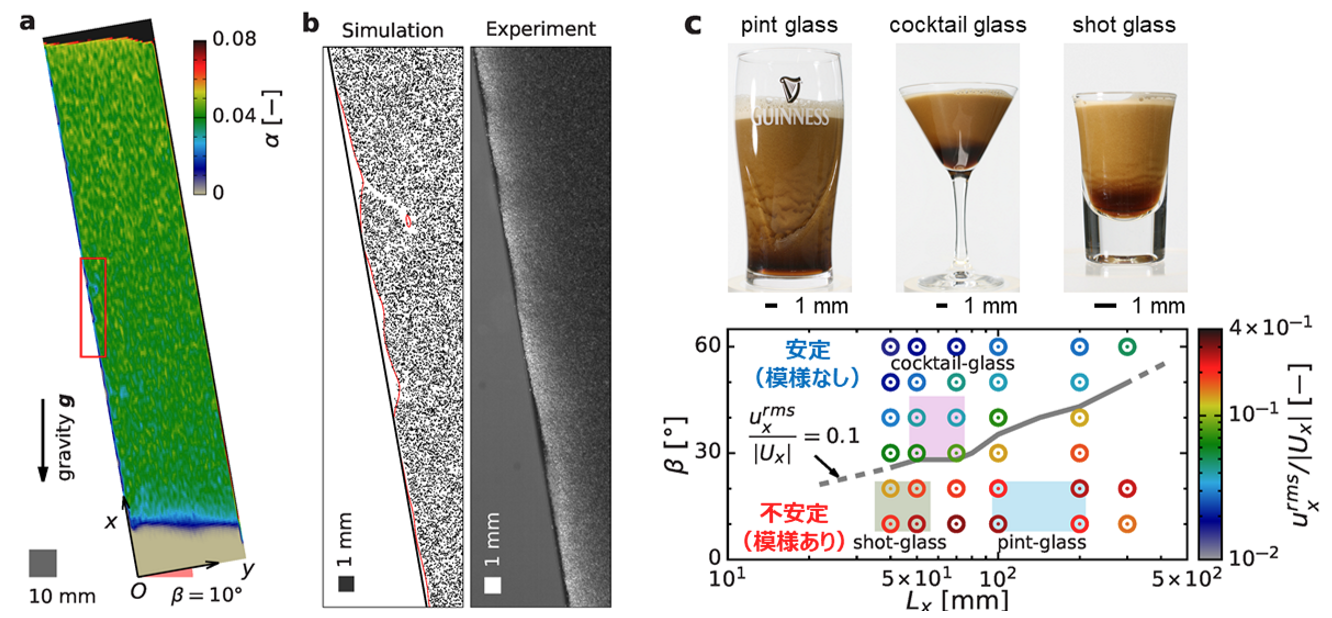
図3. 数値計算による模様の再現 (a)コップを模擬した二次元空間において泡の運動をシミュレーションしています。色は気泡の量を表しています。(b)シミュレーション(左)と実験(右)の比較。傾斜した壁の近くで泡が少なくっている様子が再現されています。(c)様々なコップにギネスビールを注ぎ模様を観察した結果(上)とシミュレーションによる模様の有無(下)。(今回の論文の補足情報として、以下のリンク先で実際の動画を入手いただけます。 https://journals.aps.org/pre/supplemental/10.1103/PhysRevE.103.063103)
本研究成果が社会に与える影響(本研究成果の意義)
小さな物体は、様々な工業装置や食品醸造装置などで扱われる泡や粒子以外にも、河川から海洋へと流出する土砂や、湖沼に生息する微生物などを含め、自然現象中に広く存在します。このような無数にある物体を「均一に混ぜる」あるいは「一か所に集める」行為は、各種工業プロセスにおいて重要な要素であり、小さな物体がどの様に運動するかを理解・制御する必要があります。今後、この知見は工業装置や食品醸造装置、細胞や微生物の培養装置などの設計方策に活用されることや、容器内部で生じる流動現象に対する物理的な理解を進展させることが期待されます。
特記事項
本研究成果は、2021年6月8日(火)午前0時(日本時間)に米国科学誌「Physical Review E」(オンライン)に掲載されました。
タイトル:“Bubble cascade may form not only in stout beers”
著者名:Tomoaki Watamura、 Kazuyasu Sugiyama、 Yuko Yotsumoto、 Mihoko Suzuki、and Hideyuki Wakabayashi
掲載誌:Physical Review E
DOI: https://doi.org/10.1103/PhysRevE.103.063103
なお、本研究の一部は、日本学術振興会科学研究費補助金の助成を受けて行われました。
参考文献
[1] Watamura, T., Iwatsubo, F., Sugiyama, K., Yamamoto, K., Yotsumoto, Y., & Shiono, T. (2019). Bubble cascade in Guinness beer is caused by gravity current instability. Scientific reports, 9(1), 1-9.
[2] Harada, S., Mitsui, T., & Sato, K. (2012). Particle-like and fluid-like settling of a stratified suspension. The European Physical Journal E, 35(1), 1-6.
[3] Koyama, M., Watamura, T., & Sugiyama, K. (2019). Simultaneous photobleaching molecular tagging velocimetry for density-stratified flows of suspensions. Experiments in Fluids, 60(9), 1-22.
参考URL
大阪大学 大学院基礎工学研究科 機能創成専攻 杉山研究室
http://flow.me.es.osaka-u.ac.jp/
SDGs目標

用語説明
- 転波(てんぱ)
傾斜面を流れ落ちる液膜表面に生じる波のことです。典型的な例として、坂道や車の窓ガラスを流れる雨水の表面にみられる波が挙げられます。
- 数理モデル
数式を用いて、世の中の現象を記述・解析することです。流体の運動を記述する数理モデルの他、感染症の流行や交通渋滞の流れといった様々な現象を対象とした数理モデルが提案されています。
- スケーリング則
二つの量の間の変換関係を主張する法則をいいます。両者が比例関係やべき乗則、指数則に従うなどを議論する場合に用います。
- フルード数
流体の慣性力と重力との比を表す無次元数のことです。主に水面に生じる波の状態を表す際に使われます。フルード数が小さいと波が生じにくく、フルード数が大きいと波が生じやすい状態となります。
- 濃度界面の解像度
泡同士の平均距離と液膜厚さの比を表す無次元数のことです。泡の浮上に伴い傾斜壁面近傍は泡のない液膜が形成されますが、この液膜に対する泡同士の平均距離を比較し、泡が密にあるかどうかの指標としています。
