グラフェンは、高い電気伝導性・熱伝導性、化学耐性、機械耐性、高効率で広帯域の光吸収特性などを持つ炭素による2次元シートです。この2次元シートを用いて離散幾何学で知られている立体的な周期的曲面構造を構築すると単純な2次元グラフェンとは異なる特性が発現し、様々な用途への展開が可能になると予測されています。

東北大学材料科学高等研究所の陳明偉教授、岡山理科大学理学部の田邉洋一准教授、筑波大学数理物質系の伊藤良一准教授らの研究グループは、炭素1個分の厚さしかない原子層物質である2次元グラフェンシートをモチーフとする3次元構造体を作製し、立体的な曲面構造を持つグラフェンが2次元グラフェンの特性を大きく上回る優れた物質であること、さらに立体的な曲面構造がグラフェンの特性にどのように影響するのかを明らかにしました。

本研究成果により様々な立体グラフェンデバイスの開発が進むことが期待されます。

本研究はドイツ科学雑誌「Advanced Materials」に2020年10月28日(現地時間)付けでオンライン掲載されました。

多種多様な立体構造を持つ炭素材料が開発され、様々な応用研究が展開されています。その中で炭素の6員環が蜂の巣状につながった2次元グラフェンの特徴を保持したまま立体的な周期構造を持たせると特異な物性や優れた特性を発揮すると言われています。例えば、表面張力の釣り合いが取れた状態は数学において「極小曲面」と呼ばれる構造を与え、熱力学的には準安定となります。これにより構造の安定性を保ちつつ総表面積の最大化が可能になり、そのような特異な幾何学構造を持つグラフェンは2次元グラフェンとは異なる特性を示すことが数学者や理論家によって予言されています。我々の研究グループでは、周期的立体構造を持つグラフェンを作製して様々なデバイス特性を評価していますが、幾何学構造と物性の結び付けは非常に難しく、本物質が持つ3次元的な曲面や疑似的な周期構造がグラフェン本来の物性をどのように変調するのかは実験的には明らかにできていませんでした。

今回、この課題に対して、意図的にグラフェンの曲がり具合を示す曲率半径を変えることによって、3次元集積化(曲面の詰め込み具合)がグラフェンの物性をどのように変えるのか、一定体積当たりどこまでの集積効率ならばグラフェンとしての特性を保持できるのかなどを検討することで、3次元の立体構造を持つグラフェンデバイスの設計指針を得ることに成功しました。

3次元グラフェンの物性を調べるうえで、我々は本物質がもつ3種類の幾何学的な特徴:(1)原子間距離の伸縮を伴う曲面、(2)トポロジカル欠陥と呼ばれるグラフェンを3次元的に曲げるために不可欠な5、7、8員環構造と(3)疑似的な周期構造に着目しました。(1)グラフェンの伸縮効果による炭素原子間の電荷の飛び移りの変調は、グラフェンの伝導電子の運動方向を変調する場(擬磁場)の発生として理解できることが知られています。従って、3次元グラフェンが持つ伸縮のある曲面上を電子が動き回ると、あたかも様々な方向に電子が散乱されるような効果が発生します。加えて、(2)トポロジカル欠陥の周りを電子が一周すると、バレーと呼ばれるグラフェンの2つの異なる電子状態間を差し渡すように電子が散乱されることが知られています。(3)周期構造をもつ3次元グラフェンの理論計算からは、周期の逆数に比例するバンドギャップ の形成が示唆されています。つまり、グラフェンに疑似的な周期構造が存在する場所では局所的にバンドギャップの形成が起こる可能性があると予想されます。本研究グループのこれまでの3次元ナノ多孔質グラフェン研究によると、曲面による電子物性の変調を示す様々な結果が観測されてきましたが、曲面の曲率が十分に高くないため、グラフェンの電子物性を大幅に変調するには至りませんでした。今回我々は、これまでで最も曲率の高い曲率半径25-50nmの試料を含む、曲率の大幅に異なる3種類の3次元ナノ多孔質グラフェン(25-50nm、50-150nm、500-1000nm、 図1 )の作製に成功し、立体的な曲面構造がグラフェンの電子物性に与える影響について調べました。

（表1） に3次元ナノ多孔質グラフェンの曲率半径に対する電気伝導度と静電容量を示します。立体的な曲面構造を持つグラフェンが2次元グラフェンと比較して巨大な表面積を持つことから、静電容量は2次元グラフェンと比較して1000倍程度増大しました。さらに、曲率半径が小さくなるにつれて静電容量が増大することから、体積あたりに含まれる総表面積が増大していることを示しています。これらは乱雑にグラフェンを配置しても得られない特性です。一方、電気伝導度は、曲率半径500-1000nmの試料において、平面状のグラフェンと比較して1000倍程度増加する一方で、曲率半径が小さくなると減少することを観測しました。従って、立体的な曲面構造を持つグラフェンにおいては、グラフェンの体積あたりの総表面積の増大に対して必ずしも電気伝導度が増大するわけではないことが明らかになりました。

図2(a) に示す角度積分光電子分光 の測定からは、グラフェンが持つ質量ゼロのディラック電子 の特徴として知られているエネルギーに対して線形な状態密度が、曲率の増大とともに減少することが明らかになりました。また、 図2(b) に示す電気二重層トランジスタ を利用した電気伝導度の測定からは、試料の幅と電圧端子間距離で規格化した電気抵抗が曲率半径の減少に対して系統的に増大するものの、スイッチング比の増大は観測されないことが分かりました。この結果は、3次元多孔構造に局所的に含まれる様々な疑似的周期構造の影響によって局所的にバンドギャップが形成されている可能性があることを示すものです。

次に、電気伝導度の温度と磁場依存性を測定した結果、ゼロ磁場中における電気伝導度が低温で温度Tに対する自然対数(logT)に比例すること、曲率半径の減少とともに、その温度領域と傾きが増大することが明らかになりました （図3(a)） 。特に、50-150nmと25-50nmの2つの試料において、定常磁場を印加した状態で電気伝導度の温度変化を測定した結果、50-150nmの試料においては、弱局在・弱反局在 と呼ばれるグラフェンのディラック電子の散乱に由来する量子干渉効果によって、電気伝導度のlogTに比例した成分が磁場に対して増減する一方で、25-50nmの試料においては、電子間のクーロン相互作用に由来する効果が支配的になることによって、電気伝導度のlogTに比例した成分が大きな変化を示さないことが明らかになりました （図3(b-d)） 。

このような曲率半径に対する電気伝導特性の変化と、立体的な曲面構造による電子散乱効果の関係を調べるために、磁気抵抗効果とラマン散乱 の測定を行った結果、25-50nmの試料において強い電子散乱の効果のために負の磁気抵抗効果が支配的になり （図4(a)） 、同時にラマン散乱においてグラフェンのバレーと呼ばれる2つの異なる電子状態内と電子状態間をそれぞれ差し渡す電子散乱に関係するD’バンドとDバンドと呼ばれる2つのピークが顕著に増大することが明らかになりました （図4(b)） 。これらをまとめると、曲率半径50-1000nmの試料においては、立体的な曲面構造による電子散乱効果は存在するものの、グラフェンの質量ゼロのディラック電子状態が持つ量子位相に由来した低散逸な電気伝導が支配的であると言えます。一方で、曲率半径25-50nmの試料においては立体的な曲面構造による高頻度な電子散乱によってディラック電子による低散逸な電気伝導が強く抑制されており、その結果として電子間のクーロン相互作用に由来する電気伝導度の補正効果が強く現れていると考えられます。

これらの研究成果から、例えば底面積が1mm ² の場合を考えて、総表面積が1mm ² の2次元グラフェンと総表面積が~1000mm ² の50-150nmの本グラフェンを比較すると、本グラフェンはグラフェンの特性を維持していることから総表面積の増大分

だけ体積あたりの性能値向上が十分に見込めるという見積もりが可能であることが分かりました。

3次元ナノ多孔質グラフェンにおける立体的な曲面構造と曲率を制御することは、簡単に言うと「一定体積当たりにどれだけの高品質なグラフェンを詰め込めたか」を意味しており、高密度に詰め込んだグラフェンを用いて得られた本研究成果は実用的立体デバイスの性能指標となるものです。つまり、本研究は、体積当たりの表面積と電気伝導性やキャリア易動度が求められるデバイス(受光素子、触媒電極やキャパシタなど)を考える上での性能指標となり、小さくかつ高密度にすればするほどよいというわけではなく、グラフェンの特性を保持できるデバイスサイズが重要であるなど、大きな設計指針を示したと言えます。従って、本研究から得られた曲率に依存した3次元グラフェンの性能値をもとにして、様々な3次元グラフェンの設計と開発が進むことが期待されます。

"Dirac Fermion Kinetics in 3D Curved Graphene"
(曲面構造を持つグラフェン上のディラック電子の動力学)
"Yoichi Tanabe, Yoshikazu Ito, Katsuaki Sugawara, Mikito Koshino, Shojiro Kimura, Tomoya Naito, Isaac Johnson, Takashi Takahashi, and Mingwei Chen, Advanced Materials 2020 , 2005838. DOI: 10.1002/adma.202005838 .

本研究成果は、東北大学大学院理学研究科/材料科学高等研究所:菅原克明准教授と高橋隆名誉教授、大阪大学大学院理学研究科:越野幹人教授、東北大学金属材料研究所:木村尚次郎准教授、東京大学大学院理学系研究科/理化学研究所仁科加速器科学研究センター:内藤智也氏、ジョンズ・ホプキンズ大学:Isaac Johnson氏との共同研究によるものです。

本研究は、JSPS科研費新学術領域研究「次世代物質探索のための離散幾何学」17H06460(総括班)、JP20H04628、科学研究費助成事業(科研費)、公益財団法人泉科学技術振興財団、世界トップレベル研究拠点プログラム(WPI)、東北大学金属材料研究所における共同研究(新素材共同研究開発センター:20G0002、強磁場超伝導材料研究センター:18H0205、19H0204、20H0011)、文部科学省委託事業ナノテクノロジープラットフォーム課題として物質・材料研究機構微細構造解析プラットフォーム(課題番号JPMXP09A20NM0013)などの支援を受けて実施されました。

図1　走査型電子顕微鏡で観察した曲率半径が異なる3次元ナノ多孔質グラフェン像
(a)曲率半径500-1000nmの多孔質グラフェンの電子顕微鏡像
(b)曲率半径50-150nmの多孔質グラフェンの電子顕微鏡像
(c)曲率半径25-50nmの多孔質グラフェンの電子顕微鏡像

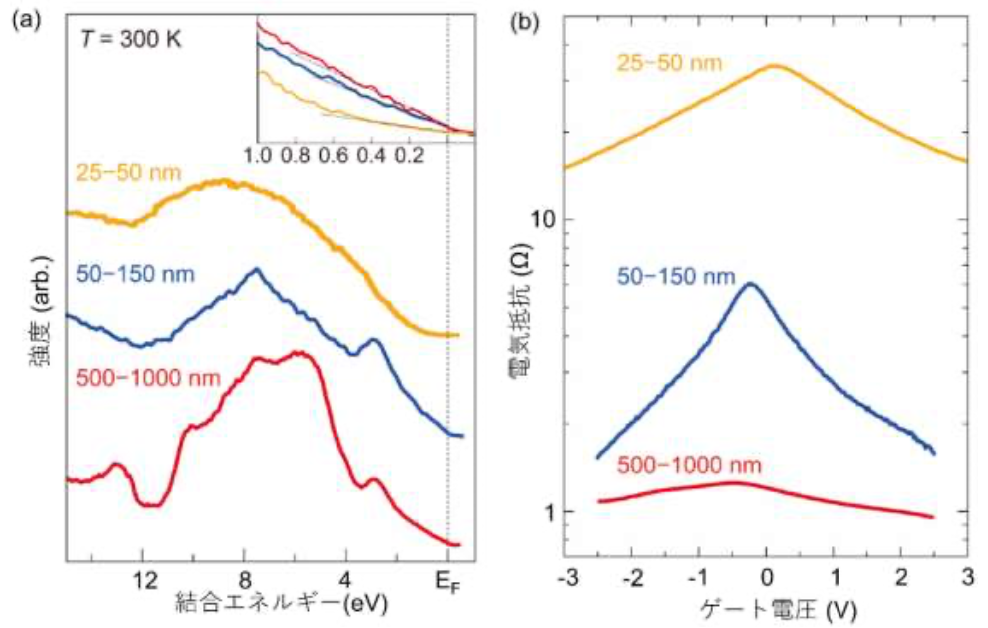
図2　曲率半径に依存した多孔質グラフェンの電子物性
(a)多孔質グラフェンの電子状態密度を反映した光電子分光スペクトル
(b)投影面積で規格化した曲率半径に依存した多孔質グラフェン電気抵抗のゲート電圧依存性

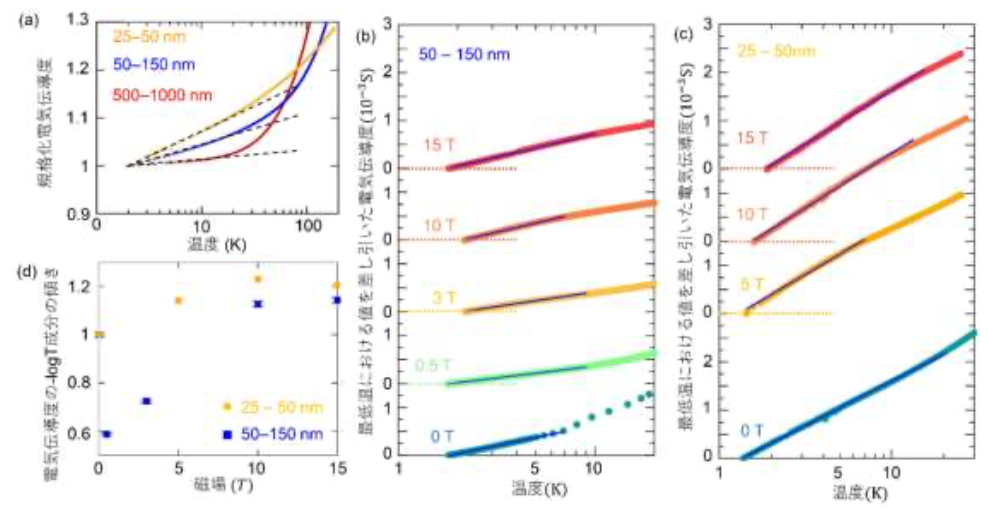
図3　曲率半径に依存した多孔質グラフェンの電子物性
(a)2Kにおける値で規格化したゼロ磁場中での電気伝導度の温度変化。横軸が対数表示になっている。
(b)(c)0-15Tの磁場中における最低温度での値を差し引いた電気伝導度の温度依存性
(d)(b)と(c)において、低温領域をAlogT+Bの近似曲線でフィッティングして求めた傾きAをゼロ磁場における値で割って定義した値の磁場依存性。50-150nmの試料では、磁場の増加に対して傾きが一度減少し、再び増大する。一方で、25-50nmの試料では、傾きの変化が減少していることが分かる。

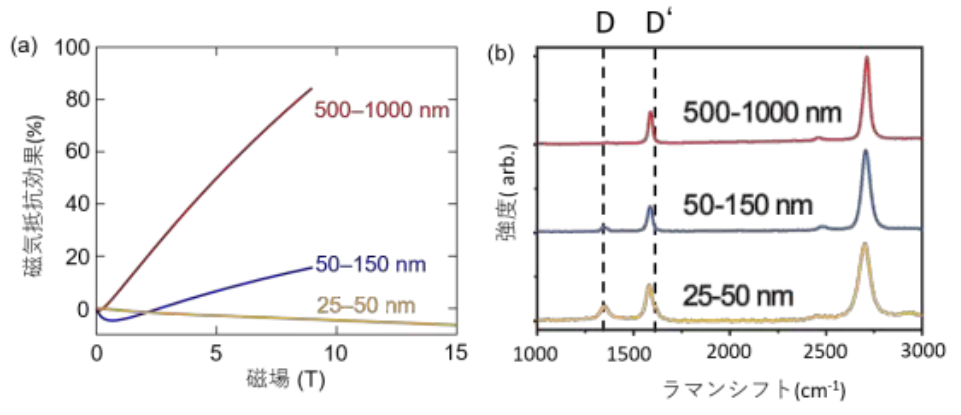
図4　曲率半径に依存した多孔質グラフェンの磁気抵抗効果とラマンスペクトル
(a)磁場に対する電気抵抗の変化をゼロ磁場における値で割って定義した2Kにおける磁気抵抗効果の磁場依存性。曲率半径の減少に対して、曲面による電子散乱の影響で負の磁気抵抗効果が支配的になる。
(b)ラマン散乱強度のエネルギーシフトに対する変化。図中のD、D’バンドはグラフェンのバレーと呼ばれる異なる電子状態間と電子状態内での電子散乱効果と関係している。

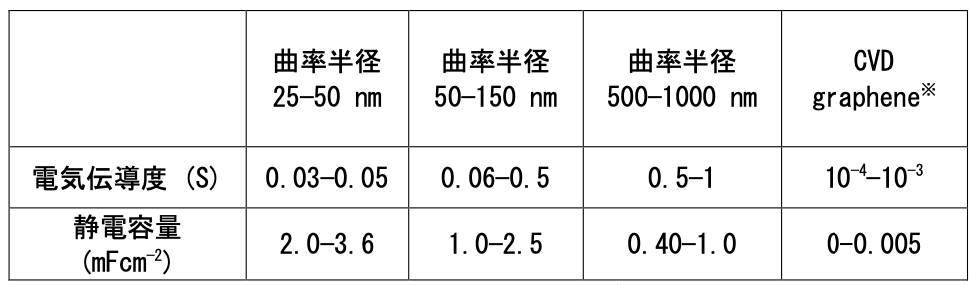
表1　曲率を変化させたときの室温での多孔質グラフェンのデバイス特性のまとめ。電気伝導度は試料の幅と電圧端子間距離で規格化している。静電容量は、平面上のグラフェンと比較するため、基板上における試料の底面積で規格化している。(※CVD (chemical vapor deposition) grapheneとは、化学気相蒸着法によるグラフェンを示す。)