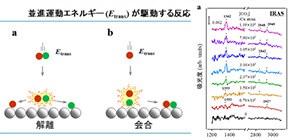
分子振動が化学反応を駆動する
銅触媒表面での二酸化炭素の水素化反応機構を解明
研究成果のポイント
・銅触媒表面における二酸化炭素の水素化反応が、二酸化炭素の振動エネルギーで駆動する化学反応であることを明らかにしました。
・本研究は、このようなタイプの反応機構について、実際の事例を見出した最初の報告です。
・これにより、二酸化炭素からメタノールを合成する触媒反応を、「状態間化学(State-to-StateChemistry)」を応用した省エネルギープロセスによって実現する道が開かれました。
研究の概要
国立大学法人筑波大学数理物質系(エネルギー物質科学研究センター)全家美博士研究員、近藤剛弘准教授、中村潤児教授らの実験グループ、および、国立大学法人大阪大学大学院工学研究科Fahdzi Muttaqien(ファージ・ムタキン)特任助教(常勤)、濱田幾太郎准教授、森川良忠教授らの理論計算グループは共同で、銅触媒表面での二酸化炭素の水素化反応が、二酸化炭素の分子振動励起によって駆動される反応であることを明らかにしました。
これまで、気体分子の振動エネルギーや並進エネルギー が、固体表面上での分子の解離反応に影響を及ぼすことは報告されてきました。また、気相分子が固体表面上の吸着種と直接衝突する会合反応においては、気体分子の並進エネルギーが反応性に影響を与える例が示されています。しかしながら、気体分子の振動エネルギーが駆動する化学反応は、報告例がありませんでした。
本研究では、気体分子の並進、振動、回転エネルギーを、系統的に制御可能な超音速分子線技術 を用いることで、銅触媒表面上での二酸化炭素の水素化反応を調べました。その結果、反応速度は二酸化炭素の振動エネルギーと共に大きく増加し、表面温度とは無関係であることが示され、分子振動で駆動する反応であることがわかりました。
本研究成果により、二酸化炭素分子に関連した様々な表面化学反応のメカニズムと速度論の理解が深まることが期待できます。また、二酸化炭素からメタノールを合成する触媒反応を、「状態間化学(State-to-State Chemistry)」を応用した省エネルギープロセスによって実現する道が開かれました。
本研究成果は、2019年6月24日付「Nature Chemistry」誌で公開されました。
*本研究は、戦略的創造研究推進事業先導的物質変換領域(ACT-C)研究領域「低エネルギー、低環境負荷で持続可能なものづくりのための先導的な物質変換技術の創出」(研究総括:國武豊喜)「二酸化炭素活性化機構の学理に基づくメタノール室温合成触媒の創成」(研究代表者:中村潤児)の研究として実施されました。
研究の背景
気相中での分子同士の化学反応の研究においては、反応時のエネルギー移動に関する理解(動力学の理解)が1970年代より急速に進みました。これに伴い、分子の特定のモードにエネルギーを供給することで化学反応を精密に制御する、いわゆる「状態間化学(state-to-state chemistry)」について多くの研究がなされてきました[1-3]。この概念を固体触媒表面上での分子間の化学反応において捉えると、「状態間触媒化学(state-to-state catalytic chemistry)」と呼ぶことができますが、この概念は、必要な所にだけエネルギーを用いるという観点から、実際に社会で使われている不均一系触媒作用を用いた化学合成プロセスのエネルギーコストを削減する上で極めて重要です。このような化学反応は、気相分子と触媒固体表面との間を熱的に非平衡な状態にすることで実現できます。実際、これまでにこのような反応やその動力学について気相中の分子の並進、振動、および回転エネルギーを系統的に制御することを可能とする超音速分子線技術と呼ばれる技術を用いることで、世界的に幅広く研究がなされてきました[4,5]。これまでに研究されてきた熱的に非平衡な気体分子と表面との反応について、 図1 に整理して示します。気体分子の並進エネルギーが駆動する解離 (図1a) と会合 (図1b) 、気体分子の振動エネルギーが駆動する解離 (図1c) と会合 (図1d) の4種類に分類することができます。このうちa-cに示した3つの反応タイプについては報告があり、詳細な動力学が最先端の量子ダイナミクス計算を含めて、詳しく研究されてきています[6-11]。しかしながら、これまで 図1 dに示す振動エネルギー駆動の結合形成反応(E-R型)についての報告はありませんでした。
これまでの研究により、銅触媒表面上でのフォルメート種 の形成反応(CO 2 +1/2H 2 →HCOO a 、「a」は吸着種を表します)がE-R型のメカニズムの反応であると示唆されてきました[12-17]。具体的には、(1)反応速度の圧力依存性が、一般的な触媒反応プロセスであるL-H型のメカニズムでは説明できないこと、(2)銅の表面構造が異なっていても、活性化エネルギーと初期反応速度がそれぞれ非常に似ていること、すなわち反応が銅の表面構造に敏感ではないことが示されてきました。また、密度汎関数理論(DFT)を用いた理論計算により、これらのユニークな速度論的特徴が、二酸化炭素が銅表面上に吸着している水素原子と直接反応するというE-R型のメカニズムによってよく説明でき、さらにO-C-Oの変角振動励起によって駆動される可能性が示されてきました。
そこで本研究では、二酸化炭素の並進や振動エネルギーが銅表面上での二酸化炭素の水素化反応に及ぼす影響を調べることによってE-R型メカニズムを検証し、二酸化炭素の活性化の動力学を明らかにすることを目的としました。
研究内容と成果
銅触媒表面でのフォルメートの生成
まず、銅触媒表面が低温であっても二酸化炭素にエネルギーを与えることで二酸化炭素の水素化反応が起きることが明確に示された結果を示します。超高真空中で180Kに冷やしたCu(111)表面に原子状水素をあらかじめ吸着させた後、並進エネルギー(E trans )を1.54eV、平均振動エネルギー(E̅ vib )を155meVに制御した二酸化炭素分子を超音速分子線として照射したところ、表面にフォルメート種が形成することが示されました。照射後の赤外反射吸収分光(IRAS、 図2a )により銅表面上に二座配位したフォルメート種が形成していることが示され、昇温脱離 (TPD、 図2b )によりフォルメートの分解脱離に由来する408Kでの水素と二酸化炭素の同時脱離が化学量論(HCOO→CO 2 +1/2H 2 )に対応する強度で観測されたことから明らかとなりました。
図2c、d 、は、それぞれIRASとTPDから見積もられる、フォルメートの生成量に対応する信号強度をプロットした結果です。二酸化炭素の導入に伴って生成量が増加して飽和するまでの挙動が一致していることがわかります。これらの曲線の初期の傾きを基に初期反応確率P 0 を求めると9×10 -4 と見積もられました。この値は、高圧下(380 Torr CO 2 、380 Torr H 2 )、353Kでの反応確率として報告[12]されている2.4×10 -12 よりもはるかに高い値です。つまり、180Kという低い表面温度(T surf )であっても、エネルギーを二酸化炭素にのみ供給することで、フォルメート種が急速に形成されることが示されました。これは、反応障壁を克服するためのエネルギーが、 図2e に概略的に示されるように、Cu(111)表面ではなく、高温の二酸化炭素分子自体から生じていることを示唆する結果です。
P0に対するTsurf 、Etrans、および Ē vib の影響
次に、P 0 に対するT surf 、E trans 、およびĒ vib の影響をCu(111)表面とCu(100)表面のそれぞれで調べました。 図3a に示した通り、P 0 はT surf が120〜220Kの範囲内において一定であり、E trans が1.47eVおよび1.97eVのときにそれぞれ0.6×10 -3 および1.8×10 -3 を示しています。つまり並進エネルギーには依存性が見られるものの、表面温度には依存性が無いことがわかります。この結果は、二酸化炭素分子がCu表面と熱的に平衡にならず、直接Haと反応するというE–R型のメカニズムを示しています。また、Cu(111)とCu(100)での結果に違いが無い点について、CO 2 とH 2 からのフォルメート生成反応が銅触媒表面の構造に影響されないという過去の実験報告[12-14]と一致していることもわかります。
図3b、c は、180KのCu(111)とCu(100)でのP 0 に対するE trans とĒ vib の影響を示しています。Ē vib を142meVで一定に保ち、E trans を1.12から1.97eVまで増加させると、E trans の増加に応じてP 0 が増加しています (図3c) 。同様に、E trans を1.30eVまたは1.56eVで一定に保ち、Ē vib を87から159meVまで増加させると、Ē vib の増加に応じてP 0 が増加します (図3c) 。これらの依存関係はCu(111)とCu(100)で似ていることもわかります。図中のデータ点の傾き(E trans やĒ vib の増加に対するP 0 の増加割合)が急な場合、エネルギー効率が高いことを意味します。Ē vib での傾き( 図3c より∆logP 0 /∆Ē vib ≒13.4eV -1 )は、E trans の傾き( 図3b より∆logP 0 /∆E trans ≒1.6-2.0eV -1 )よりはるかに(P 0 の増加割合の違いとしてみると約11桁も)大きいため、反応障壁を克服するためにはĒ vib がE trans よりもはるかに効率的であることがわかります。さらに、η=∆E trans /∆Ē vib としてエネルギー効率ηを求めたところ7.9と見積もられました。これはNi表面でのCH 4 (η=0.5-1.4)の解離反応[9,18]やH 2 O(η=1.1)の解離反応[19]について報告された値と比較して非常に大きいことがわかります。このような、二酸化炭素分子の反応に対する振動エネルギーの著しい有効性は、これまでに観察されたことがない結果です。
P0に対する二酸化炭素のEtransの表面垂直方向成分および表面平行方向成分の影響
P 0 に対するE trans の表面垂直方向成分(E n =E trans cos 2 θ i )の効果を 図4 に示します。様々な入射角度θ i で測定した結果をプロットしていますが、P 0 がE n と共に単調に増加していることがわかります。つまり、P 0 はE trans の表面垂直方向成分によって決定され、E trans の表面平行方向成分は反応に関わっていないことがわかります。これは、二酸化炭素が表面と衝突する際、E n の一部が遷移状態と同様の二酸化炭素の分子構造に変形するためのエネルギーとして使用され、反応障壁を克服していることを示唆しています。0.52–0.60eVのしきい値エネルギー(E thresh )は、高圧実験でのフォルメート生成に関して過去に報告[12,13]されている活性化エネルギー(E act )0.58eVと近い値となっています。これは、E n がCO 2 の変形のために使われている、すなわちCu上でフォルメートを形成するのに必要な分子構造の変形のためのエネルギーに変換されていることを強く支持する結果です。
単一衝突のE–R型の反応メカニズム
E-R型反応として、単一衝突による直接反応モデルと、多重衝突を伴う物理吸着を介するトラッピングモデル、の2つのモデルが考えられます。 図3 、 4 の結果は、二酸化炭素と吸着水素との単一衝突で反応が起きていることを示しています。具体的には、①二酸化炭素の並進エネルギー(E trans >1eV)がCu表面上の物理吸着ポテンシャルの深さ(0.2eV)よりもはるかに高いため、多重衝突を伴う反応は除外することができること、②P 0 がしきい値を超えるとE n と共に急激に増加する結果 (図4) が、トラッピングモデルでは説明できないこと、③ 図4 で示した結果のうち、入射角度が大きくなるにつれてP 0 が減少する点がトラッピングモデルと矛盾すること、から単一衝突で反応が起きていることがわかります。ただしこのことは、本研究で実験をしていない、低いE trans と高いĒ vib 条件で反応が進行する反応チャンネルが存在する可能性を除外するものではありません。
密度汎関数法(DFT)による第一原理計算を用いたシミュレーション
二酸化炭素には3つの振動モード(対称伸縮、非対称伸縮、変角)があるため、どの振動モードが分子の活性化に関与しているのかを明確にすることが重要です。ファンデルワールス密度汎関数を用いて計算した、二酸化炭素と吸着水素との反応によるCu(111)上のフォルメート生成の最小エネルギー経路を 図5 に示します。 図5b-d の斜線部分で示すように、反応座標は、(i)ファンデルワールス(vdW)引力 段階(緑の陰影)、(ii)パウリ反発 段階(青の陰影)、および(iii)反応ステージ(赤の陰影)、の3つの重要な段階で構成されています。第一段階では、二酸化炭素はHa/Cu(111)に近づき、表面から約3.40Åの距離で物理吸着するまでvdW引力の影響を受けます。第二段階として、物理吸着した二酸化炭素がHa/Cu(111)に近づく一方で、ポテンシャルエネルギーは反応座標に沿って0.30eV増加します。この際、O-C-O結合角度とCO結合距離はあまり変化しません (図5b-d) 。従って、ここでのエネルギー上昇は、二酸化炭素分子と表面との間のパウリ反発力に起因すると考えられます。その後、第三段階としてO−C−O結合角度が減少し始め、遷移状態で144.6°となります。気相の二酸化炭素の場合(表面から隔離されている場合)、分子のエネルギーは、O-C-O角度を144.6°に曲げると0.89eV増加します。しかしながら、この表面反応では、曲がった二酸化炭素分子は、O−Cu結合を形成する前に遷移状態でのC−H結合形成によって部分的に安定化されるため、フォルメート形成のE act は0.55eVとなります。この計算で導かれたE act は実験データ(0.58eV)[12,13]とよく一致しています。このように、 図5 の結果は明らかにE-R型の反応メカニズムを示しており、E act は主に二酸化炭素の変角振動モードによるものであることを示しています。
二酸化炭素の変角振動駆動の反応過程をさらに検証するため、初期状態から遷移状態まで、二酸化炭素のO-C-O角度を144.6°に固定してフォルメート生成反応の経路を計算した結果を 図5e に示します。気相における初期の二酸化炭素は、直線分子構造の場合よりも0.89eV安定性が低く、吸着された水素との反応が、障壁なしで実現できることがわかります。つまり、変角振動励起を伴う二酸化炭素分子が銅表面上に吸着した水素と反応することが示されました。
動力学と速度論の関係
本研究で見出された反応動力学の知見により、工業的条件下での触媒反応速度論の特徴をより深く理解することができます。高圧下(380 Torr CO 2 、380 Torr H 2 )、353Kでの銅触媒上でのフォルメート生成反応は、E act が0.58eVとそれほど大きくないにもかかわらず、反応確率P bulb は2.4×10 と非常に小さいことが報告されています[12]。これらを用いてアレニウスの式 ※8 P bulb =ν e ∙exp(–E act /RT)より前指数因子ν e を見積もると6×10 -4 という値となります。これはCu(110)上のH 2 の解離反応やNi(100)上でのCH 4 の解離反応について報告されているν e (それぞれ約1および0.44)よりはるかに小さい値です。すなわち、フォルメート生成反応における非常に低いP bulb は、小さいν e に由来するものであるといえます。本研究で得られた知見を踏まえると、この小さいν e は限られた衝突構造でのみ反応が進行することを示しており、二酸化炭素分子が折れ曲がり、かつ二酸化炭素分子の中心の炭素原子が銅触媒表面の水素原子と衝突するという条件を満たしたときにのみ反応が起こることを示していると理解できます。
本研究で得られたP 0 のĒ vib 依存性データを用いて、振動温度353KかつE trans =0eVでの初期反応確率を見積もると5×10 -12 となり、353Kの反応温度で高圧実験により見積もられた値(2.4×10 -12 )と近いことがわかりました。このことは、CO 2 の振動エネルギーが、工業的反応条件下でのフォルメート生成における反応速度を決定することを意味しています。工業的条件下の高圧実験ではフォルメートの生成速度はCu触媒の温度に依存しますが[12]、本研究では、 図3a で示した通り銅表面の温度に依存しませんでした。本研究で得られた他のエネルギー依存性を踏まえると、工業条件下の高圧実験では触媒の加熱により触媒と衝突する二酸化炭素分子も加熱されるため、分子の振動温度も増加していることになり、見かけ上、触媒温度依存性が確認されていると理解することができます。
今後の展開
本研究の成果により、二酸化炭素分子に関連した様々な表面化学反応のメカニズムと速度論の理解が深まることが期待できます。また、二酸化炭素からメタノールを合成する触媒反応を「状態間化学(Stateto-State Chemistry)」を応用した省エネルギープロセスによって実現する道が開かれました。
参考図
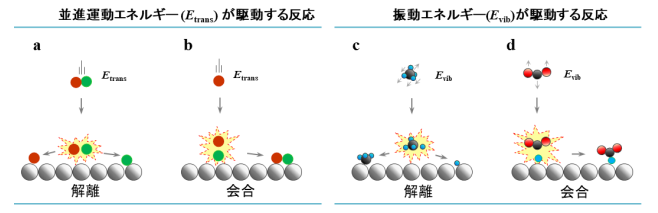
図1 4種類の熱的に非平衡な気体分子と表面との反応
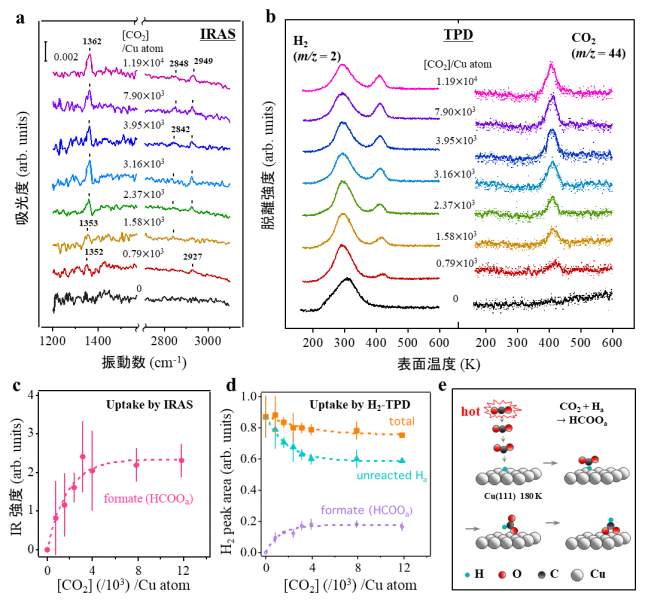
図2 表面温度180KのHa/Cu(111)とCO 2 分子線(E trans =1.54eV、Ē vib =155meV)との反応によるフォルメート生成
赤外反射吸収分光法(IRAS)と昇温脱離法(TPD)により様々なCO 2 曝露量(Cu原子当たりのCO 2 衝突数:[CO 2 ]/Cu原子)における反応生成物とその量を特定
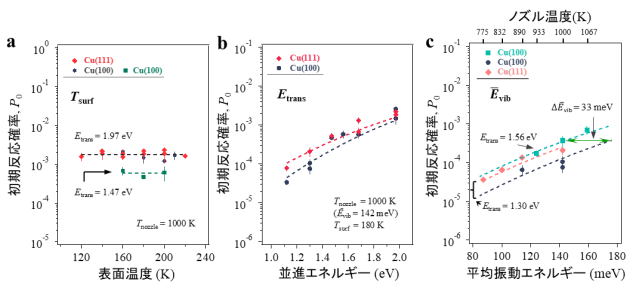
図3 Cu(111)およびCu(100)におけるフォルメート生成の初期反応確率(P 0 )に及ぼす表面温度(T surf )、CO 2 並進エネルギー(E trans )、およびCO 2 平均振動エネルギー(Ē vib )の影響(分子線入射角度θ i =0°)
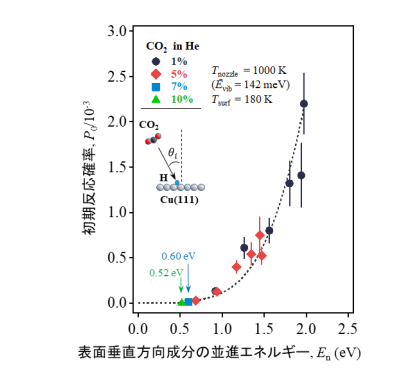
図4 P 0 に対するCO 2 並進エネルギーの表面垂直方向成分(E n )の影響(表面温度180K、Ē vib =142meV)
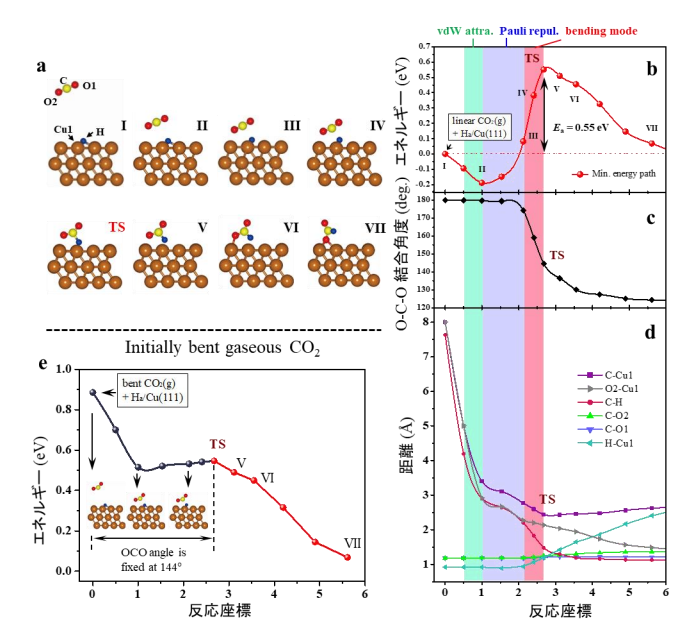
図5 第一原理計算によるCu(111)上でのCO 2 水素化によるフォルメート生成の反応経路
参考文献
[1] Polanyi, J. C. Acc. Chem. Res. 5, 161–168 (1972).
[2] Lee, Y. T. Science 236, 793–798 (1987).
[3] Liu, K. Annu. Rev. Phys. Chem. 67, 91–111 (2016).
[4] Kleyn, A. W. Chem. Soc. Rev. 32, 87–95 (2003).
[5] Gross, A. et al. in The Chemical Physics of Solid Surfaces Vol. 11 (ed Woodruff D. P.)1–378 (Elsevier, 2003).
[6] Michelsen, H. A., Rettner, C. T. & Auerbach, D. J. in Surface Reactions (ed Madix R. J.)185–237 (Springer, 1994).
[7] Hayden, B. E. in Dynamics of gas-surface interactions (eds Rettner C. T. & Ashfold M. N.R.) 137–170 (The Royal Society of Chemistry, 1991).
[8] Rettner, C. T. Phys. Rev. Lett. 69, 383–386 (1992).
[9] Juurlink, L. B. F., Killelea, D. R. & Utz, A. L. Prog. Surf. Sci. 84, 69–134 (2009).
[10] Díaz, C. et al. Science 326, 832–834 (2009).
[11] Nattino, F. et al. J. Phys. Chem. Lett. 5, 1294–1299 (2014).
[12] Nakano, H., Nakamura, I., Fujitani, T. & Nakamura, J. Phys. Chem. B 105, 1355–1365(2001).
[13] Nakamura, J., Kushida, Y., Choi, Y., Uchijima, T. & Fujitani, T. J. Vac. Sci. Technol.A 15, 1568–1571 (1997).
[14] Taylor, P. A., Rasmussen, P. B., Ovesen, C. V., Stoltze, P. & Chorkendorff, I. Surf.Sci. 261, 191–206 (1992).
[15] Wang, G., Morikawa, Y., Matsumoto, T. & Nakamura, J. J. Phys. Chem. B 110, 9–11 (2006).
[16] Muttaqien, F., Oshima H., Hamamoto Y., Inagaki K., Hamada I., and Morikawa Y., Chem.Commun. 53, 9222–9225 (2017).
[17] Quan, J., Kondo, T., Wang, G. & Nakamura, J. Angew. Chem. Int. Ed. 56, 3496–3500(2017).
[18] Smith, R. R., Killelea, D. R., DelSesto, D. F. & Utz, Science 304, 992–995 (2004).
[19] Hundt, P. M., Jiang, B., vanReijzen, M. E., Guo, H. & Beck, R. D. Science 344, 504–507(2014).
掲載論文
【題 名】 Vibration-driven reaction of CO 2 on Cu surfaces via Eley–Rideal-type mechanism
(Eley‐Rideal 型機構による Cu 表面上の CO 2 の振動駆動反応)
【著者名】 Jiamei Quan, Fahdzi Muttaqien, Takahiro Kondo, Taijun Kozarashi, Tomoyasu Mogi,Takumi Imabayashi, Yuji Hamamoto, Kouji Inagaki, Ikutaro Hamada, Yoshitada Morikawa,Junji Nakamura
【掲載誌】 Nature Chemistry (DOI: 10.1038/s41557-019-0282-1)
参考URL
大阪大学 大学院工学研究科 精密科学・応用物理学専攻 精密科学コース 計算物理領域 森川研究室
http://www-cp.prec.eng.osaka-u.ac.jp/#
用語説明
- 並進エネルギー
分子の並進運動に伴うエネルギー。
- 超音速分子線技術
速度や方向が揃い、且つ強度が大きい真空中を直進する中性分子の流れを超音速分子線と呼び、これを制御する技術を指す。混合する気体の質量や線源の温度を制御することで分子線を構成する気体分子の並進、振動、回転エネルギーを制御することができる。
- フォルメート種
ここでは銅表面上に吸着しているHCOO種を指す。銅系触媒上において二酸化炭素からメタノールを合成する際に形成される重要な中間体であることが知られている。
- 昇温脱離
昇温脱離計測 (TPD):
試料表面にガスを曝したのちに試料を加熱し、表面に吸着したガスが試料表面から脱離してくる量と脱離する温度を測定する。これにより、ガスの吸着エネルギーや脱離速度、吸着確率、脱離のメカニズムなどを解析することができる。
- 第一原理計算
第一原理電子状態計算:
物質中の電子の状態を、量子力学の基本法則に基づいて精密に求める計算手法。
- ファンデルワールス(vdW)引力
電子雲の量子力学的揺らぎによって生じる分子―分子あるいは分子―表面間の引力的相互作用
- パウリ反発
1つの量子状態を複数の電子が占有することはできないとするパウリの排他原理に由来する斥力的相互作用。ここでは分子軌道と基板の波動関数の重なりによって斥力的相互作用が生じ、その結果エネルギーが上昇したことを指している。
- アレニウスの式
化学反応速度定数kと絶対温度Tとの関係を表わす式。
